题目内容
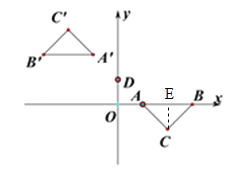
【题目】如图,在平面直角坐标系中,点A,B,D的坐标为(1,0),(3,0),(0,1),点C在第四象限,∠ACB=90°,AC=BC.若△ABC与△A'B'C'关于点D成中心对称,则点C'的坐标为______.

【答案】(-2,3)
【解析】分析:过C作CE⊥AB于E,由A、B的坐标,可得AB的长,由等腰三角形的性质得到BE,AE,CE的长,从而得到点C的坐标,再根据待定系数法,可得直线DA的函数解析式,根据中点坐标公式,可得答案.
详解:过C作CE⊥AB于E.
∵∠ACB=90°,AC=BC,∴E为AB的中点,∴CE=![]() AB.
AB.
∵A(1,0),B(3,0),∴E(2,0),AB=2,CE=AE=BE=1,∴C(2,-1).
设DA的解析式为y=kx+b,将A,D点坐标代入,得:
![]() ,解得
,解得![]() ,AD的解析式为y=﹣x+1.
,AD的解析式为y=﹣x+1.
设C′的坐标为(x,y),则D为CC′的中点.由中点坐标公式,得:
x+2=0,y-1=2,解得:x=-2,y=3.∴C′(-2,3).故答案为:(﹣2,3).

练习册系列答案
相关题目