Question

【题目】如图，AB是⊙O的直径，弦CD⊥AB于点G，点F是CD上一点，且满足 = ，连接AF并延长交⊙O于点E，连接AD，DE，若CF=2，AF=3，给出下列结论：①△ADF∽△AED；②FG=2；③tanE= ；④S△DEF=4 ，其中正确的是（ ）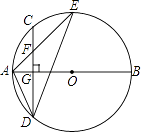
A.①②③
B.②③④
C.①②④
D.①③④

Answer 1

【答案】C
【解析】解：①∵AB是⊙O的直径，弦CD⊥AB， ∴ ，DG=CG，
∴∠ADF=∠AED，
∵∠FAD=∠DAE（公共角），
∴△ADF∽△AED；
故①正确；
②∵ = ，CF=2，
∴FD=6，
∴CD=DF+CF=8，
∴CG=DG=4，
∴FG=CG﹣CF=2；
故②正确；
③∵AF=3，FG=2，
∴AG= = ，
∴在Rt△AGD中，tan∠ADG= = ，
∴tan∠E= ；
故③错误；
④∵DF=DG+FG=6，AD= = ，
∴S△ADF= DFAG= ×6× =3 ，
∵△ADF∽△AED，
∴ =（ ）2 ，
∴ = ，
∴S△AED=7 ，
∴S△DEF=S△AED﹣S△ADF=4 ；
故④正确．
故选C．
①正确．由AB是⊙O的直径，弦CD⊥AB，根据垂径定理可得： ，DG=CG，继而证得△ADF∽△AED；
②正确．由 = ，CF=2，可求得DF的长，继而求得CG=DG=4，则可求得FG=2；
③错误．由勾股定理可求得AG的长，即可求得tan∠ADF的值，继而求得tan∠E= ．
④首先求得△ADF的面积，由相似三角形面积的比等于相似比的平方，即可求得△ADE的面积，继而求得S△DEF=4 ．