题目内容
【题目】如图,MN是⊙O的直径,MN=4,∠AMN=30°,点B为弧AN的中点,点P是直径MN上的一个动点,则PA+PB的最小值为( ) 
A.2
B.2 ![]()
C.4 ![]()
D.4
【答案】B
【解析】解:过A作关于直线MN的对称点A′,连接A′B,由轴对称的性质可知A′B即为PA+PB的最小值, 连接OB,OA′,AA′,
∵AA′关于直线MN对称,
∴ ![]() ,
,
∵∠AMN=30°,
∴∠A′ON=60°,∠BON=30°,
∴∠A′OB=90°,
过O作OQ⊥A′B于Q,
在Rt△A′OQ中,OA′=2,
∴A′B=2A′Q=2 ![]() ,
,
即PA+PB的最小值2 ![]() .
.
故选B.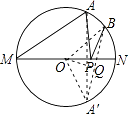
【考点精析】本题主要考查了圆周角定理的相关知识点,需要掌握顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半才能正确解答此题.

练习册系列答案
相关题目