��Ŀ����
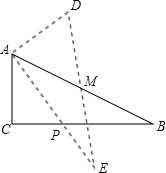
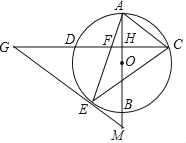
����Ŀ��������ABCD�У�����AB����ֱ���Ƶ�A��ʱ����תһ���Ƕ����õ�ֱ��AM������C��CE��AM������ΪE������BE��
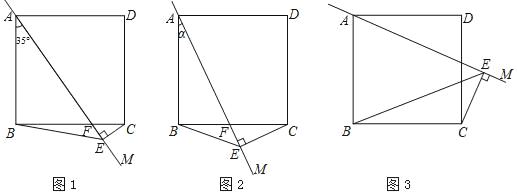
��1����0��������45��ʱ����AM��BC�ڵ�F��
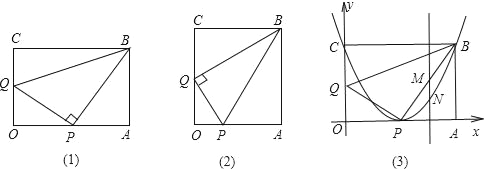
����ͼ1��������35�������BCE���� ������
����ͼ2���õ�ʽ��ʾ�߶�AE��BE��CE֮���������ϵ����֤����
��2����45��������90��ʱ����ͼ3������ֱ���õ�ʽ��ʾ�߶�AE��BE��CE֮���������ϵ��
���𰸡���1����35����AE��CE+![]() BE��֤������������2��AE+CE��
BE��֤������������2��AE+CE��![]() BE�����ɼ�����.
BE�����ɼ�����.
��������
��1�����ı���ABCD��������ͨ���ǵĹ�ϵ�����AFB��CE��AM�����������BCE.
�ڹ���B��BG��BE����AM�ڵ�G���ɢ����ı���ABCD���������á�ABG����CBE����ͨ��ֱ���������ڽǺʹ������ɵõ���������BCE������ABG�ա�CBE��ASA������ͨ�����ɶ������ɵó�AE��CE��![]() BE.
BE.
��2������B��BG��BE����AM�ڵ�G���ɣ�1���еõ���ABG����CBE����ͨ��ֱ���������ڽǺʹ������ɵõ���DAH����DCE���ӳ�DA��BG��N���á�BAG����BCE�����ɵõ���ABG�ա�CBE��ASA������ͨ�����ɶ���GE��![]() BE�������������ɵó�AE��BE��CE֮���������ϵ.
BE�������������ɵó�AE��BE��CE֮���������ϵ.
��1���١��ı���ABCD�������Σ����ABC��90����
�ߡ�BAF��35����
���AFB��90������BAF��55����
���CFE����AFB��55����
��CE��AM��
���CEF��90����
���ECF��90������CFE��35����
������BCE��35����
�ʴ�Ϊ��35��
��AE��CE��![]() BE��
BE��
֤������ͼ2������B��BG��BE����AM�ڵ�G��
���GBE����GBC����CBE��90����
���ı���ABCDΪ�����Σ�
��AB��BC����ABC����ABG����GBC��90����
���ABG����CBE��
�ߡ�ABC��90����
���������AFB��90����
�ߡ�CFE����AFB��
���������CFE��90����
�ߡ�CEF��90����
���BCE����CFE��90����
���������BCE��
����ABG����CBE��
��ABG����CBE��AB��BC����������BCE��
���ABG�ա�CBE��ASA����
��AG��CE��BG��BE��
����Rt��BEG��BG��BE��
��GE��![]() BE��
BE��
��AE��AG��GE��CE��![]() BE��
BE��
��2�����ɣ���ͼ3������B��BG��BE����AM�ڵ�G��
���GBE����GBA����ABE��90����
���ı���ABCDΪ�����Σ�
��AB��BC����D����ABC����ABE����EBC��90����
���ABG����CBE��
�ߡ�D��90����
���DAH����AHD��90����
�ߡ�AHD����CHE��
���DAH����CHE��90����
�ߡ�CEA��90����
���DCE����CHE��90����
���DAH����DCE��
�ӳ�DA��BG��N��
�ߡ�NAG����DAH�����NAG����DCE��
���NAG��90������DCE��90����
���BAG����BCE
����ABG����CBE��
��ABG����CBE��AB��BC����BAG����BCE��
���ABG�ա�CBE��ASA����
��AG��CE��BG��BE��
����Rt��BEG��BG��BE��
��GE��![]() BE��
BE��
��AE��GE��AG��![]() BE��CE��
BE��CE��
����AE��CE��![]() BE��
BE��


 �������ϵ�д�
�������ϵ�д�