��Ŀ����
����Ŀ��������Сܿ��Ƶ�����Բ��һ������֪Բ���������ij߹���ͼ���̣�
��֪����O����O��һ��P��
��������O��һ�����ߣ�ʹ�������߾�����P��
������������OP����OP�Ĵ�ֱƽ����l��
��OP�ڵ�A��
����AΪԲ�ģ�AOΪ�뾶��Բ��
����O�ڵ�M��
����ֱ��PM����ֱ��PM��Ϊ��O�����ߣ�
����Сܿ��Ƶij߹���ͼ���̣�
��1��ʹ��ֱ�ߺ�Բ�棬��ȫͼ�Σ���������ͼ�ۼ���
��2����������֤����
֤��������OM��
����ͼ��֪��AΪOP�е㣬
��OPΪ��Aֱ����
���OMP���� ���������� �����������������ݣ�
��OM��PM��
�֡ߵ�M�ڡ�O�ϣ�
��PM�ǡ�O�����ߣ����� �����������������ݣ�
���𰸡���1����ͼ����������2��֤��������.
��������
��1����Ҫ����ͼ.
��2������Բֱ�������ʡ����ߵ��ж���������֤������.
�⣺��1����ȫͼ�Σ���ͼ��ʾ��
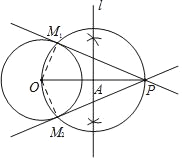
��2��֤��������OM��
����ͼ��֪��AΪOP�е㣬
��OPΪ��Aֱ����
���OMP��90������ֱ�����Ե�Բ�ܽ���ֱ�ǣ���
��OM��PM��
�֡ߵ�M�ڡ�O�ϣ�
��PM�ǡ�O�����ߣ��������뾶����˲��Ҵ�ֱ�������뾶��ֱ����Բ�����ߣ���
�ʴ�Ϊ��90��ֱ�����Ե�Բ�ܽ���ֱ�ǣ������뾶����˲��Ҵ�ֱ�������뾶��ֱ����Բ�����ߣ�

 �ο�ͨ�γ̱�˼ά����������ѵ��ϵ�д�
�ο�ͨ�γ̱�˼ά����������ѵ��ϵ�д�