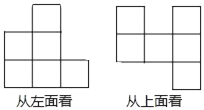
题目内容
【题目】有理数a、b、c在数轴上对应点的位置如图:① abc<0;② (a-b)(b-c)(c-a)>0;③|a|<1-bc;④|a-b|+|b-c|=|a-c|;以上四个结论正确的有( )个.
![]()
A.4B.3C.2D.1
【答案】B
【解析】
观察数轴上a、b、c的位置,可得出![]() ,可对①作出判断;由a-b<0,b-c<0,c-a>0,可对②作出判断;根据
,可对①作出判断;由a-b<0,b-c<0,c-a>0,可对②作出判断;根据![]() ,1-bc<1,可对③作出判断;分别化简|a-b|+|b-c|和|a-c|,可对④作出判断,就可得出正确结论的个数.
,1-bc<1,可对③作出判断;分别化简|a-b|+|b-c|和|a-c|,可对④作出判断,就可得出正确结论的个数.
根据题意可得:![]() ,∴abc<0,①正确;
,∴abc<0,①正确;
∵a-b<0,b-c<0,c-a>0,∴(a-b)(b-c)(c-a)>0,②正确;
∵![]() ,1-bc<1,∴|a|>1-bc,③错误;
,1-bc<1,∴|a|>1-bc,③错误;
∵![]() ,
,
∴|a-b|+|b-c|=-a+b-b+c=-a+c,|a-c|=-a+c,
∴|a-b|+|b-c|=|a-c|,④正确。∴正确的有3个,故选B.

练习册系列答案
相关题目