��Ŀ����
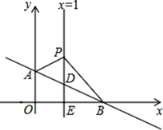
����Ŀ����ͼ��ƽ��ֱ������ϵ�У�ֱ��AB:y= -![]() +b��y���ڵ�A(0,1),��x���ڵ�B,ֱ��x=1��AB�ڵ�D,��x���ڵ�E,P��ֱ��x=1�ϵ�һ���㣬���ڵ�D���Ϸ�����P(1,n).
+b��y���ڵ�A(0,1),��x���ڵ�B,ֱ��x=1��AB�ڵ�D,��x���ڵ�E,P��ֱ��x=1�ϵ�һ���㣬���ڵ�D���Ϸ�����P(1,n).
(1)��ֱ��ABd����ʽ�͵�B�����ꣻ
(2)���ABP�����(�ú�n�Ĵ���ʽ��ʾ)��
(3) ��![]() =2ʱ,
=2ʱ,
�������P�����ꣻ���ڢٵ������£���PBΪ���ڵ�һ����������ֱ�ǡ�BPC��ֱ��д����C�����꣮
���𰸡�(1) y=��![]() x+1, ��B��3��0��;(2)
x+1, ��B��3��0��;(2) ![]() n��1;(3)��P(1��2)���ڣ�3��4����5��2����3��2��.
n��1;(3)��P(1��2)���ڣ�3��4����5��2����3��2��.
��������
(1)����A���������ֱ��AB�Ľ���ʽ�����bֵ���ɵ�AB�Ľ���ʽ���̶���y=0�������Ӧ��xֵ���ɵõ�ΪB�����ꣻ
(2)����A��AM��PD������ΪM�����AM�ij����������BPD����PAD����������ߵĺͼ�Ϊ��ABP�������
(3)�ٵ�S��ABP=2ʱ������������õĴ���ʽ�����nֵ��������õ�P�����ꣻ
�ڷ�P��ֱ�Ƕ�����BP=PC��B��ֱ�Ƕ�����BP=BC ��C��ֱ�Ƕ�����CP=CB����������C�����꼴�ɣ�
(1)��y=��![]() x+b����A(0��1)����b=1��
x+b����A(0��1)����b=1��
��ֱ��AB�Ľ���ʽ��y=��![]() x+1��
x+1��
��y=0ʱ��0=��![]() x+1�����x=3�����B(3��0)��
x+1�����x=3�����B(3��0)��
(2)����A��AM��PD������ΪM������AM=1��

��x=1ʱ��y=��![]() x+1=
x+1=![]() �� P�ڵ�D���Ϸ�����PD=n��
�� P�ڵ�D���Ϸ�����PD=n��![]() ��
��
S��APD=![]() PDAM=
PDAM=![]() ��1��(n��
��1��(n��![]() )=
)=![]() n��
n��![]() ��
��
�ɵ�B(3��0)����֪��B��ֱ��x=1�ľ���Ϊ2��
����BDP�ı�PD�ϵĸ߳�Ϊ2��
��S��BPD=![]() PD��2=n��
PD��2=n��![]() ��
��
��S��PAB=S��APD+S��BPD=![]() n��
n��![]() +n��
+n��![]() =
=![]() n��1��
n��1��
(3)�ٵ�S��ABP=2ʱ��![]() n��1=2�����n=2�����P(1��2)��
n��1=2�����n=2�����P(1��2)��
�ڡ�E(1��0)��
��PE=BE=2��
���EPB=��EBP=45����
��1���������ͼ1����CPB=90����BP=PC��
����C��CN��ֱ��x=1�ڵ�N��

�ߡ�CPB=90������EPB=45����
���NPC=��EPB=45����
����CNP����BEP��
 ��
��
���CNP�ա�BEP��
��PN=NC=EB=PE=2��
��NE=NP+PE=2+2=4��
��C(3��4)��
��2���������ͼ2����PBC=90����BP=BC��
����C��CF��x���ڵ�F��

�ߡ�PBC=90������EBP=45����
���CBF=��PBE=45����
����CBP����PBE��
 ��
��
���CBF�ա�PBE��
��BF=CF=PE=EB=2��
��OF=OB+BF=3+2=5��
��C(5��2)��
��3���������ͼ3����PCB=90����CP=CB��
���CPB=��CBP=45����

�ߡ�EPB=��EBP=45����
���PCB=��CBE=��EPC=90����
���ı���EBCPΪ���Σ�
��CP=CB��
���ı���EBCPΪ�����Σ�
��PC=CB=PE=EB=2��
��C(3��2)��
����PBΪ���ڵ�һ����������ֱ��������BPC����C��������(3��4)��(5��2)��(3��2)��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�