Question

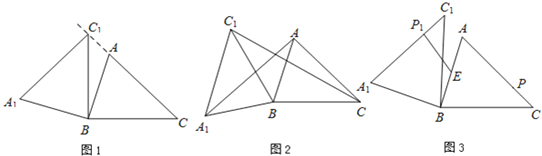
【题目】如图1，△ABC中，∠C＝90°，若AC＝6，BC＝8，AD平分∠CAB交CB于D．

（1）求CD的长；

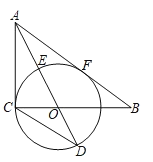
（2）如图2，E是AC上一点，连ED，过D作DE的垂线交AB于F，若ED＝DF，求CE的长；

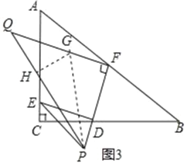
（3）如图3，在（2）条件下，点P在FD延长线上，过F作ED的平行线QF，连PE、PQ，若∠QPF＝2∠PED＝2α，PQ＝5PD，（QF＞PF），求QF．

Answer 1

【答案】（1）CD＝3；（2）CE＝1；（3）QF＝．

【解析】

（1）过点D作DE⊥AB于E，根据角平分线上的点到角的两边距离相等可得CD＝DE，利用勾股定理列式求出AB，然后根据S△ABC＝S△ACD+S△ABD列方程求解即可．

（2）过F作FG⊥BC于G，证明：△CDE≌△GFD，△BGF∽△BCA，即可求解；

（3）过P作∠QPF的平分线交FQ于G，过G作GH⊥PQ于H，证明Rt△PFG≌Rt△PHG，△PED∽△GPF，设PD＝x，建立方程求解即可．

（1）如图1，过点D作DE⊥AB于E，

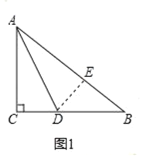
∵∠ACB＝90°，AD平分∠CAB，

∴CD＝DE，

在△ABC中由勾股定理得：AB＝＝10，

∵S△ABC＝S△ACD+S△ABD，

∴×AC×BC＝×AC×CD+×AB×DE，即×6×8＝×6×CD+×10×CD，

解得：CD＝3；

（2）如图2，过F作FG⊥BC于G，则∠C＝∠FGD＝90°，

∵DE⊥DF，

∴∠EDF＝90°，

∴∠CDE+∠CED＝∠CDE+∠FDG＝90°，

∴∠CED＝∠FDG，

在△CDE与△GFD中

，

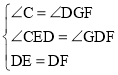∴△CDE≌△GFD（AAS），

∴CE＝DG，FG＝CD＝3，

∵FG∥AC，

∴△BGF∽△BCA，

∴＝，

∴BG＝4，

∴CE＝DG＝1；

（3）如图3，在Rt△CDE中，DE＝DF＝＝，

∵PQ＝5PD，∴设PD＝x，则PQ＝5x，

∴PF＝+x，过P作∠QPF的平分线交FQ于G，过G作GH⊥PQ于H，

∵FQ∥DE，∴∠QFP＝∠EDP＝90°，

∴GH＝GF，在Rt△PFG与Rt△PHG中，，

∴Rt△PFG≌Rt△PHG（HL），

∴PH＝PF＝+x，

∵∠QPF＝2∠PED＝2∠FPG＝2α，

∴∠PED＝∠FPG，

∴△PED∽△GPF，

∴＝，即＝，

∴FG＝，

∴HG＝FG＝，

∵QH＝PQ﹣PH＝4x﹣，

∴QG＝，FQ＝QG+FG＝，

∵△QGH∽△QPF

∴＝，即GHFQ＝PFQG

∴×＝（+x）×，解得：x1＝（舍去），x2＝，

∴QF＝．