题目内容
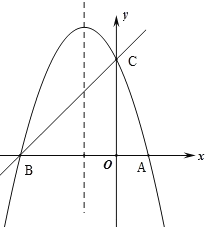
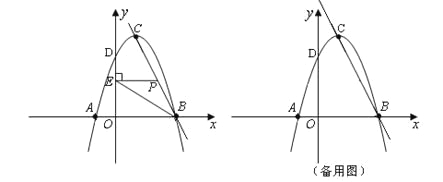
【题目】如图,在直角坐标系中,抛物线![]() 与y轴交于点D(0,3).
与y轴交于点D(0,3).
(1)直接写出c的值;
(2)若抛物线与x轴交于A、B两点(点B在点A的右边),顶点为C点,求直线BC的解析式;
(3)已知点P是直线BC上一个动点,
①当点P在线段BC上运动时(点P不与B、C重合),过点P作PE⊥y轴,垂足为E,连结BE.设点P的坐标为(x,y),△PBE的面积为s,求s与x的函数关系式,写出自变量x的取值范围,并求出s的最大值;
②试探索:在直线BC上是否存在着点P,使得以点P为圆心,半径为r的⊙P,既与抛物线的对称轴相切,又与以点C为圆心,半径为1的⊙C相切?如果存在,试求r的值,并直接写出点P的坐标;如果不存在,请说明理由.
【答案】(1)c=3;(2)![]() ;(3)①S=-x2+3x=-(x-
;(3)①S=-x2+3x=-(x-![]() )2+
)2+![]() (1<x<3);当x=
(1<x<3);当x=![]() 时,S取得最大值,最大值为
时,S取得最大值,最大值为![]() ;②存在点P1(
;②存在点P1(![]() ),或P2(
),或P2(![]() ),此时r1=
),此时r1=![]() ;点P3(
;点P3(![]() ),或P4(
),或P4(![]() ),此时r2=
),此时r2=![]() ,理由见解析.
,理由见解析.
【解析】
(1)将点D(0,3)直接代入解析式即可;
(2)先求出顶点C坐标为(1,4),以及与x轴的交点坐标,即令y=0时,得到点B(3,0)代入一次函数解析式即可求得答案;
(3)根据S=![]() PE·OE,利用P点在线段BC上,可表示出PE,OE,得到S=
PE·OE,利用P点在线段BC上,可表示出PE,OE,得到S=![]() ,变形为顶点式后求出最大值即可.第②小问,根据两圆内切与外切进行分类讨论,分别用r表示出CQ,PQ,CP的长度,再利用勾股定理即可求出r长度和P点坐标.
,变形为顶点式后求出最大值即可.第②小问,根据两圆内切与外切进行分类讨论,分别用r表示出CQ,PQ,CP的长度,再利用勾股定理即可求出r长度和P点坐标.
解:(1)∵将D(0,3)代入解析式
∴c=3
(2)由(1)知抛物线为:
y=-x2+2x+3,配方得y=-(x-1)2+4
∴顶点C坐标为(1,4)
令y=0,得x1=-1,x2=3
∴ B(3,0)
设直线BC解析式为:![]() (
(![]() ),把B、C两点坐标代入,
),把B、C两点坐标代入,
得![]() 解得
解得![]() .
.
∴直线BC解析式为![]()
(3)①∵点P(x,y)在![]() 的图象上,
的图象上,
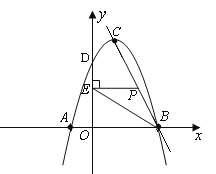
∴PE=x,OE=-2x+6
∴s=![]() PE·OE=
PE·OE=![]()
∴![]()
![]() .
.
∵x=![]() 符合1<x<3,
符合1<x<3,
∴当x=![]() 时,S取得最大值,最大值为
时,S取得最大值,最大值为![]() .
.
②答:存在.
如图,设抛物线的对称轴交x轴于点F,则CF=4,BF=2
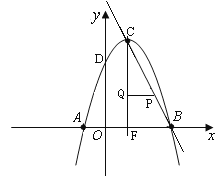
过P作PQ⊥CF于Q,则Rt△CPQ∽Rt△CBF
∴![]() ,即
,即![]()
∴CQ=2r
当⊙P与⊙C外切时,CP=r+1
∵CQ2+PQ2=CP2
∴(2r)2+r2=(r+1)2
解得r=![]() (r=
(r=![]() 舍去)
舍去)
此时P1(![]() ),或P2(
),或P2(![]() )
)
当⊙P与⊙C内切时,CP=r-1.
∵CQ2+PQ2=CP2
∴(2r)2+r2=(r-1)2
解得r=![]() (r=
(r= ![]() 舍去)
舍去)
此时P3(![]() ),或P4(
),或P4(![]() ).
).
∴当r1=![]() , r2=
, r2=![]() 时,⊙P与⊙C相切.
时,⊙P与⊙C相切.
点P的坐标为P1(![]() ),或P2(
),或P2(![]() ),
),
P3(![]() ),或P4(
),或P4(![]() ).
).