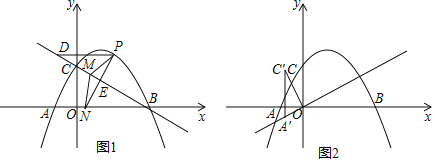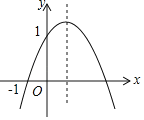题目内容
【题目】若直线![]() 与函数
与函数![]() 的图象有唯一公共点,则
的图象有唯一公共点,则![]() 的值为__ ;有四个公共点时,
的值为__ ;有四个公共点时,![]() 的取值范围是_
的取值范围是_
【答案】-3 ![]()
【解析】
根据函数y=|x2-2x-3|与直线y=x+m的图象之间的位置关系即可求出答案.
解:作出y=|x2-2x-3|的图象,如图所示,
∴y=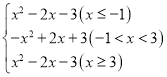 ,
,
当直线y=x+m与函数y=|x2-2x-3|的图象只有1个交点时,
直线经过点(3,0),将(3,0)代入直线y=x+m,
得m=-3,
联立![]() ,
,
消去y后可得:x2-x+m-3=0,
令△=0,
可得:1-4(m-3)=0,
m=![]() ,
,
即m=![]() 时,直线y=x+m与函数y=|x2-2x-3|的图象只有3个交点,
时,直线y=x+m与函数y=|x2-2x-3|的图象只有3个交点,
当直线过点(-1,0)时,
此时m=1,直线y=x+m与函数y=|x2-2x-3|的图象只有3个交点,
∴直线y=x+m与函数y=|x2-2x-3|的图象有四个公共点时,m的范围为:![]() ,
,
故答案为:-3,![]() .
.
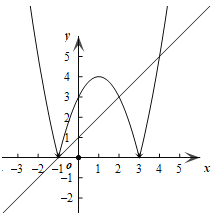

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
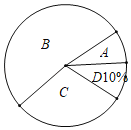
【题目】嘉善县将开展以“珍爱生命,铁拳护航”为主题的交通知识竞赛,某校对参加选拔赛的若干名同学的成绩按A,B,C,D四个等级进行统计,绘制成如下不完整的频数统计表和扇形统计图
成绩等级 | 频数(人数) | 频率 |
A | 4 | 0.08 |
B | m | 0.52 |
C | n | |
D | ||
合计 | 1 |
(1)求m= ,n= ;
(2)在扇形统计图中,求“C等级”所对应圆心角的度数;
(3)“A等级”的4名同学中有3名男生和1名女生,现从中随机挑选2名同学代表学校参加全县比赛,请用树状图法或列表法求出恰好选中“一男一女”的概率.