题目内容
【题目】如图1,在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() .
.
(1)如图1,若点![]() 是直线
是直线![]() 上方抛物线上的一个动点,过点
上方抛物线上的一个动点,过点![]() 作
作![]() 轴交直线
轴交直线![]() 于点
于点![]() ,作
,作![]() 于点
于点![]() ,点
,点![]() 为直线
为直线![]() 上一动点,点
上一动点,点![]() 为
为![]() 轴上一动点,连接
轴上一动点,连接![]() ,
,![]() .当
.当![]() 最长时,求
最长时,求![]() 的最小值;
的最小值;
(2)如图2,将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得
得![]() ,将
,将![]() 沿直线
沿直线![]() 平移得到
平移得到![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() ,将
,将![]() 沿边
沿边![]() 翻折得
翻折得![]() ,连接
,连接![]() ,
,![]() ,当
,当![]() 是等腰三角形时,求此时点
是等腰三角形时,求此时点![]() 的坐标.
的坐标.
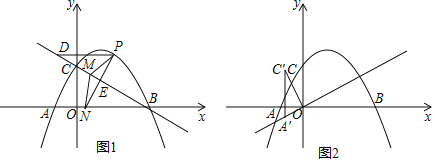
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() 或
或![]() .
.
【解析】
(1)先求出A、B、C的坐标,直线BC解析式,可推出![]() ,设
,设![]() ,则
,则![]() ,推出
,推出![]() 时
时![]() 取得最大值,此时
取得最大值,此时![]() 最长,作直线
最长,作直线![]() ,过点
,过点![]() 作
作![]() 于
于![]() ,交
,交![]() 于
于![]() ,交
,交![]() 轴于
轴于![]() ,将
,将![]() 转化为PK即可求值;
转化为PK即可求值;
(2)设![]() ,则
,则![]() ,
,![]() ,分别表示出
,分别表示出![]() ,
,![]() ,
,![]() ,再分别讨论两边相等,建立方程求解.
,再分别讨论两边相等,建立方程求解.
(1)令![]() ,得
,得![]() 或4,
或4,
令![]() 得
得![]()
∴![]() ,
,![]() ,
,![]()
BC=![]()
设直线BC解析式为:![]() ,代入
,代入![]() ,
,![]() 得:
得:
![]() ,解得
,解得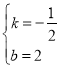
∴直线BC解析式为![]()
∵![]() ,
,![]() 轴,
轴,
∴∠PDE=∠CBO
∵∠PED=∠COB=90°
∴△PDE∽△CBO
∴![]()
∴![]() ,当
,当![]() 取得最大值时,线段
取得最大值时,线段![]() 最长.
最长.
设![]() ,则
,则![]()
∴![]()
∵![]()
∴当![]() ,即
,即![]() 时
时![]() 取得最大值,此时
取得最大值,此时![]() 最长
最长
作直线![]() ,过点
,过点![]() 作
作![]() 于
于![]() ,交
,交![]() 于
于![]() ,交
,交![]() 轴于
轴于![]() ,与y轴交于F,
,与y轴交于F,
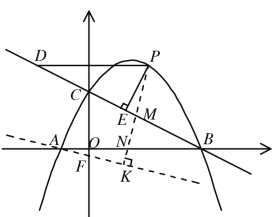
易得F点坐标为![]() ,
,
∴
∵∠OAF=∠KAN,∠AOF=∠AKN=90°
∴△AOF∽△AKN
∴![]() ,则
,则![]()
此时![]() ,
,
PK的长即为![]() 的最小值,
的最小值,
∵![]()
∴设直线PK的解析式为![]() ,将
,将![]() 代入得:
代入得:
![]() ,解得
,解得![]() ,即直线PK解析式为
,即直线PK解析式为![]()
联立![]() 与
与![]() 得:
得:
解得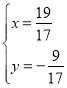 ,则M坐标为
,则M坐标为![]()
∴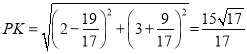
即![]() 的最小值为
的最小值为![]() .
.
(2)设![]() ,则
,则![]() ,
,![]()

∵![]()
∴![]()
![]()
![]()
当![]() 时,
时,![]() ,
,![]() 或
或![]()
当![]() 时,
时,![]() ,
,![]()
当![]() 时,
时,![]() ,
,![]()
∴![]() 或
或![]() 或
或![]()
∴![]() 或
或![]() 或
或![]()

练习册系列答案
相关题目
【题目】已知:二次函数![]() 中的
中的![]() 和
和![]() 满足下表:
满足下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)请直接写出m的值为_________.
(2)求出这个二次函数的解析式.
(3)当![]() 时,则y的取值范围为______________________________.
时,则y的取值范围为______________________________.