题目内容
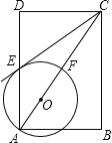
【题目】如图,在矩形ABCD中,点O在对角线AC上,以OA的长为半径的圆O与AD,AC分别交于点E,F,且∠ACB=∠DCE.
(1)判断直线CE与⊙O的位置关系,并证明你的结论;
(2)若AB=2,BC=4,求⊙O的半径.
【答案】(1)直线CE与⊙O相切,理由见解析;(2)⊙O的半径是![]()
【解析】
(1)首先连接OE,由OE=OA与四边形ABCD是矩形,易求得∠DEC+∠OEA=90°,即OE⊥EC,即可证得直线CE与⊙O的位置关系是相切;
(2)首先易证得△CDE∽△CBA,然后根据相似三角形的对应边成比例,即可求得DE的长,又由勾股定理即可求得AC的长,设⊙O的半径为R,在Rt△COE中,CO2=CE2+OE2,即可得方程(2![]() -R)2=R2+(
-R)2=R2+(![]() )2,解此方程即可求得⊙O的半径.
)2,解此方程即可求得⊙O的半径.
(1)直线CE与⊙O相切.
证明:连接OE,
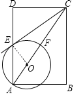
∵OA=OE,
∴∠DAC=∠AEO,
∵∠ACB=∠DCE,
∴∠AEO=∠ACB=∠DCE,
∵四边形ABCD是矩形,
∴BC∥AD,
∴∠ACB=∠DAC,
∵∠ACB=∠DCE,
∴∠DAC=∠DCE,
∵四边形ABCD是矩形,
∴∠D=90°,
∴∠DCE+∠DEC=90°,
∴∠AEO+∠DEC=90°,
∴∠OEC=180°-90°=90°,
即OE⊥EC,
∵OE为半径,
∴直线CE与⊙O相切;
(2)解:∵四边形ABCD是矩形,
∴∠B=∠D=90°,
在Rt△ACB中,AB=BC×tan∠ACB=4×![]() =2,
=2,
由勾股定理得:AC=![]() =2
=2![]() ,
,
∵∠ACB=∠DCE,
∴tan∠DCE=tan∠ACB=![]() ,
,
在Rt△DCE中,CD=AB=2,
DE=DC×tan∠DCE=2×![]() =1,
=1,
由勾股定理得:CE=![]() =
=![]() ,
,
设⊙O的半径为R,
在Rt△COE中,CO2=CE2+OE2,
(2![]() -R)2=(
-R)2=(![]() )2+ R2,
)2+ R2,
解得:R=![]() ,
,
即⊙O的半径是![]() .
.

 通城学典默写能手系列答案
通城学典默写能手系列答案