题目内容
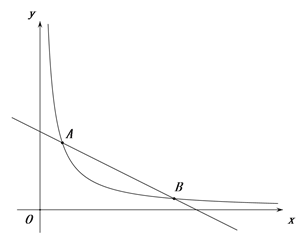
【题目】如图，已知抛物线y＝﹣x2＋bx＋c交y轴于点A（0,4），交x轴于点B（4,0），点P是抛物线上一动点，过点P作x轴的垂线PQ，过点A作AQ⊥PQ于点Q，连接AP．
（1）填空：抛物线的解析式为 ，点C的坐标 ；
（2）点P在抛物线上运动，若△AQP∽△AOC，求点P的坐标.
【答案】（1）y＝﹣x2＋3x＋4，（－1,0）（2）点P的坐标为（
，
）或（
，
）
【解析】分析：（1）把A、B的坐标代入抛物线解析式，即可求得b、c的值，从而得到抛物线的解析式．令y=0，解方程可求得点C的坐标．
（2）由点A、点C的坐标，得到
．设P（m， ﹣m2＋3m＋4）．分两种情况讨论：
①当点P在直线AQ下方时，QP＝4－（﹣m2＋3m＋4）＝ m2－3m，
由△AQP∽△AOC得：
，即：
，解方程即可得到结论．
当
时，﹣m2＋3m＋4＝，此时点P的坐标为（
）；
②当点P在直线AQ上方时，PQ＝﹣m2＋3m＋4－4＝﹣m2＋3m，
由△AQP∽△AOC得：，即：
，解方程即可得到结论．
详解：（1）∵抛物线y＝﹣x2＋bx＋c交y轴于点A（0，4），交x轴于点B（4，0），
∴
，解得：
，∴抛物线的解析式为：y＝﹣x2＋3x＋4．
令y=0，得：﹣x2＋3x＋4=0，解得：x=4或x=－1，∴点C的坐标为（－1，0）．
（2）∵点A的坐标为（0，4），点C的坐标为（－1，0），∴．
∵点P的横坐标为m，∴P（m， ﹣m2＋3m＋4）．
①当点P在直线AQ下方时，QP＝4－（﹣m2＋3m＋4）＝ m2－3m，
由△AQP∽△AOC得：，即：，
∴
（舍去）或
．
当时，﹣m2＋3m＋4＝，此时点P的坐标为（）；
②当点P在直线AQ上方时，PQ＝﹣m2＋3m＋4－4＝﹣m2＋3m，
由△AQP∽△AOC得：，即：，
∴
＝0（舍去）或
＝，此时P点坐标为（
）．
综上所述：点P的坐标为（）或（）．
【题目】据《北京晚报》介绍，自2009年故宫博物院年度接待观众首次突破1000万人次之后，每年接待量持续增长，到2018年突破1700万人次，成为世界上接待量最多的博物馆．特别是随着《我在故宫修文物》、《上新了，故宫》等一批电视文博节目的播出，社会上再次掀起故宫热．于是故宫文创营销人员为开发针对不同年龄群体的文创产品，随机调查了部分参观故宫的观众的年龄，整理并绘制了如下统计图表．
2018年参观故宫观众年龄频数分布表
年龄x/岁 | 频数/人数 | 频率 |
20≤x＜30 | 80 | b |
30≤x＜40 | a | 0.240 |
40≤x＜50 | 35 | 0.175 |
50≤x＜60 | 37 | c |
合计 | 200 | 1.000 |
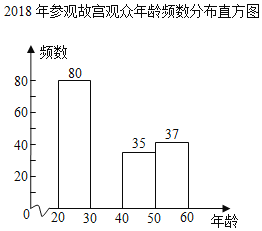
（1）求表中a，b，c的值；
（2）补全频数分布直方图；
（3）从数据上看，年轻观众（20≤x＜40）已经成为参观故宫的主要群体．如果今年参观故宫人数达到2000万人次，那么其中年轻观众预计约有 万人次．
