题目内容
【题目】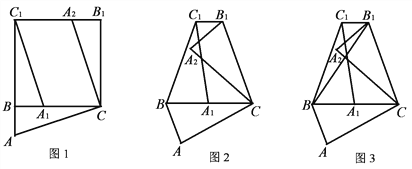
（1）如图1，在Rt△ABC中，∠ABC=90°，以点B为中心，把△ABC逆时针旋转90°，得到△A1BC1；再以点C为中心，把△ABC顺时针旋转90°，得到△A2B1C，连接C1B1，则C1B1与BC的位置关系为_______；
（2）如图2，当△ABC是锐角三角形，∠ABC=α（α≠60°）时，将△ABC按照（1）中的方式旋转α，连接C1B1，探究C1B1与BC的位置关系，写出你的探究结论，并加以证明；
（3）如图3，在图2的基础上，连接B1B，若C1B1=
BC，△C1BB1的面积为4，则△B1BC的面积为 ．
【答案】（１）平行.（２）详解解析；（３）１０
【解析】试题分析：（1）由旋转的性质可得∠C1BC=∠B1BC=90°，BC1=BC=CB1，根据平行线的判定方法可得BC1∥CB1，根据平行线的判定即可判定四边形BCB1C1是平行四边形，由平行四边形的性质即可得到结论；（2）C1B1∥BC，过C1作C1E∥B1C，交BC于E，由平行线的性质可得∠C1EB=∠B1CB，再由旋转的性质可得BC1=BC=B1C，∠C1BC=∠B1CB，即可得∠C1BC=∠C1EB，由等腰三角形的性质可得C1B=C1E，所以C1E=B1C，即可判定四边形C1ECB1是平行四边形，由平行四边形的性质即可得到结论；（3）已知C1B1∥BC，可得C1B1与BC 之间的距离相等，设这个距离为h，则△C1BB1的面积为
C1B1×h，△B1BC的面积为
CB×h，又因C1B1=
BC，△C1BB1的面积为4，即可得△B1BC的面积为10.
试题解析：
（1）平行.
（2）C1B1∥BC；
证明：过C1作C1E∥B1C，交BC于E，则∠C1EB=∠B1CB，
由旋转的性质知，BC1=BC=B1C，∠C1BC=∠B1CB，
∴∠C1BC=∠C1EB，
∴C1B=C1E，
∴C1E=B1C，
∴四边形C1ECB1是平行四边形，
∴C1B1∥BC；
（3）答案为：10．
