��Ŀ����
����Ŀ����ͼ������ABCD�У�AB��CD����ABC=90����AB=8��CD=6��BC=4��AB������һ����P������A��B�غϣ�������DP����PQ��DP��ʹ��PQ���߶�BC�ڵ�E����AP=x��
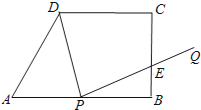
��1����xΪ��ֵʱ����APD�ǵ��������Σ�
��2������BE=y����y����x�ĺ�����ϵʽ��
��3����BC�ij�a���Ա仯�������ڵ������£��Ƿ���ڵ�P��ʹ��PQ������C���������ڣ���˵�����ɣ������ڣ�д����BC�ij���ʲô��Χ��ʱ�����Դ��������ĵ�P��ʹ��PQ������C���������Ӧ��AP�ij���
���𰸡���1����xΪ2![]() ��4��5ʱ����APD�ǵ��������Σ�
��4��5ʱ����APD�ǵ��������Σ�
��2��![]() ��
��
��3��![]()
��������
�����������1����ʾ��PH��Ȼ��֢ٵ�AP=ADʱ���ڵ�AD=PDʱ�����ݵ������������ߺ�һ�����ʣ�AH=PH����ʽ���м��㼴�ɵý⣻�۵�AP=PDʱ����ʾ��PH��Ȼ����Rt��DPH�У����ݹ��ɶ�����ʽ���м��㼴�ɵý⣻
��2������ͬ�ǵ������������HDP=��EPB���ٸ������Ƕ�Ӧ��ȣ������������������DPH����PEB���ƣ�Ȼ��������������ζ�Ӧ�߳ɱ����г�����ʽ�������ɵý⣻
��3������PQ����Cʱ��BE=4�����루2����BE�ı���ʽ���ٸ���һԪ���η��̵Ľ�ȷ�����ɣ�
�⣺��1����D����DH��AB��H�����ı���DHBCΪ���Σ�
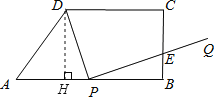
��DH=BC=4��HB=CD=6��
��AH=2��AD=2![]() ��
��
��AP=x��
��PH=x��2��
����٣���AP=ADʱ����x=2![]() ��
��
����ڣ���AD=PDʱ����AH=PH��
��2=x��2��
���x=4��
����ۣ���AP=PDʱ����Rt��DPH�У�x2=42+��x��2��2��
���x=5��
��2��x��8��
����xΪ2![]() ��4��5ʱ����APD�ǵ��������Σ�
��4��5ʱ����APD�ǵ��������Σ�
��2���ߡ�DPE=��DHP=90����
���DPH+��EPB=��DPH+��HDP=90����
���HDP=��EPB��
���ߡ�DHP=��B=90����
���DPH�ס�PEB��
��![]() ��
��
��![]() ��
��
�����ã�![]() ��
��
��3�����ڣ�
�ɣ�2������DPH�ס�PEB��
��![]() ��
��
��y=![]() ��
��
��y=aʱ����8��x����x��2��=a2����x2��10x+��16+a2��=0����=100��4��16+a2����0��
��100��64��4a2��0��
��a2��9��
����a��0��
��0��a��3��
����BC����0��BC��3ʱ�����ڵ�P��ʹ��PQ����C��
��ʱ��AP�ij�Ϊ![]() ��
��

 �����ҵ���������ϵ�д�
�����ҵ���������ϵ�д� �����̸�Ӯ����ٸ�Ч�����ܸ�ϰ���ϿƼ�������ϵ�д�
�����̸�Ӯ����ٸ�Ч�����ܸ�ϰ���ϿƼ�������ϵ�д� �����ҵ�����������ѧ���ӳ�����ϵ�д�
�����ҵ�����������ѧ���ӳ�����ϵ�д� ����ѧ��Ӯ�����ϵ�д�
����ѧ��Ӯ�����ϵ�д�