题目内容
【题目】如图,已知二次函数![]() 的图像经过点A(-1,-1)和点B(3,-9).
的图像经过点A(-1,-1)和点B(3,-9).
(1)求该二次函数的表达式;
(2)写出该抛物线的对称轴及顶点坐标;
(3)点P(m,m)与点Q均在该函数图像上(其中m>0),且这两点关于抛物线的对称轴对称,求m的值及点Q 到x轴的距离.
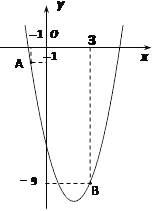
【答案】(1)y=x2﹣4x﹣6;(2)对称轴为x=2;顶点坐标为(2,﹣10);(3)m=6,点Q到x轴的距离为46.
【解析】试题分析:(1)利用待定系数法确定二次函数的解析式;
(2)把(1)中得到的解析式配成顶点式,然后根据二次函数的性质确定顶点坐标和对称轴.
(3)将P(m,m)坐标代入y=x2﹣4x﹣6,得m=m2﹣4m﹣6,解方程求得m的值,根据题意得到m=6,从而求得P的坐标,根据点P与点Q关于对称轴x=2对称,所以点Q到x轴的距离为6.
解:(1)将A(﹣1,﹣1)和点B(3,﹣9)代入y=ax2﹣4x+c,
得![]() 解得
解得![]() ,
,
所以二次函数的表达式为y=x2﹣4x﹣6;
(2)由y=x2﹣4x﹣6=(x﹣2)2﹣10可知:
对称轴为x=2;顶点坐标为(2,﹣10);
(3)将P(m,m)坐标代入y=x2﹣4x﹣6,得m=m2﹣4m﹣6.
解得m1=﹣1,m2=6.
因为m>0,所以m=﹣1不合题意,舍去.所以m=6,
所以P点坐标为(6,6);
因为点P与点Q关于对称轴x=2对称,所以点Q到x轴的距离为46.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目