题目内容
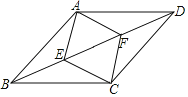
【题目】如图:点E、F为线段BD的两个三等分点,四边形AECF是菱形,且菱形AECF的周长为20,BD为24,则四边形ABCD的面积为( )
A.24B.36C.72D.144
【答案】C
【解析】
根据菱形的对角线互相垂直平分可得AC⊥BD,AO=OC,EO=OF,再求出BO=OD,证明四边形ABCD是菱形,根据菱形的四条边都相等求出边长AE,根据菱形的对角线互相平分求出OE,然后利用勾股定理列式求出AO,再求出AC,最后根据四边形的面积等于对角线乘积的一半列式计算即可得解.
解:如图,连接AC交BD于点O,
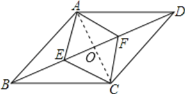
∵四边形AECF是菱形,
∴AC⊥BD,AO=OC,EO=OF,
又∵点E、F为线段BD的两个三等分点,
∴BE=FD,
∴BO=OD,
∵AO=OC,
∴四边形ABCD为平行四边形,
∵AC⊥BD,
∴四边形ABCD为菱形;
∵四边形AECF为菱形,且周长为20,
∴AE=5,
∵BD=24,点E、F为线段BD的两个三等分点,
∴EF=8,OE=![]() EF=
EF=![]() ×8=4,
×8=4,
由勾股定理得,AO=![]() =
=![]() =3,
=3,
∴AC=2AO=2×3=6,
∴S四边形ABCD=![]() BDAC=
BDAC=![]() ×24×6=72;
×24×6=72;
故选:C.

 习题精选系列答案
习题精选系列答案【题目】中央电视台的“朗读者”节目激发了同学们的读书热情,为了引导学生“多读书,读好书”,某校对八年级部分学生的课外阅读量进行了随机调查,整理调查结果发现,学生课外阅读的本数最少的有5本,最多的有8本,并根据调查结果绘制了不完整的图表:
本数(本) | 人数(人数) | 百分比 |
5 | a | 0.2 |
6 | 18 | 0.36 |
7 | 14 | b |
8 | 8 | 0.16 |
合计 | c | 1 |
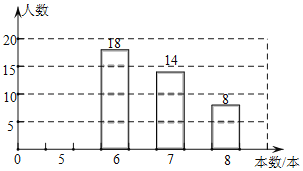
根据以上提供的信息,解答下列问题:
(1)a=_____,b=_____,c=______;
(2)补全上面的条形统计图;
(3)若该校八年级共有1200名学生,请你分析该校八年级学生课外阅读7本及以上的有多少名?