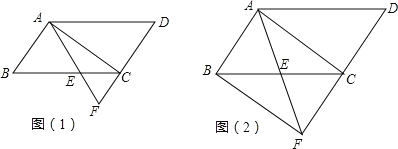
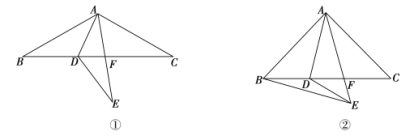
题目内容
【题目】在![]() 中,
中,![]() ,点
,点![]() 是
是![]() 上一点,沿直线
上一点,沿直线![]() 将
将![]() 折叠得到
折叠得到![]() ,
,![]() 交
交![]() 于点
于点![]() .
.
(1)如图①,若![]() ,求
,求![]() 的度数;
的度数;
(2)如图②,若![]() ,
,![]() ,连接
,连接![]() ,判断
,判断![]() 的形状,并说明理由.
的形状,并说明理由.
【答案】(1)52°;(2)△ABE是等边三角形,理由见解析.
【解析】
(1)根据翻折变换的性质得到∠ADB=∠ADE,根据邻补角的概念求出∠ADC即可解答;
(2)设∠EDC=∠DAB=x,用x表示出∠ADB和∠ADE,根据翻折变换的性质列出方程,解方程求出x,再根据三角形外角的性质求出∠DBE,得到∠ABE=60°即可证得结论.
解:(1)∵∠ADB=116°,
∴∠ADE=116°,∠ADC=180°116°=64°,
∴∠EDC=∠ADE∠ADC=52°;
(2)△ABE是等边三角形,
理由:∵∠BAC=90°,AB=AC,
∴∠ABC=∠C=45°,
设∠EDC=∠DAB=x,则∠ADB=180°45°x,∠ADE=45°+x+x,
∴180°45°x=45°+x+x,
解得:x=30°,
∵∠EDC=30°,DB=DE,
∴∠DBE=∠DEB=15°,
∴∠ABE=60°,
又∵AB=AE,
∴△ABE是等边三角形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
【题目】某体育用品商店一共购进20个篮球和排球,进价和售价如下表所示,全部销售完后共获得利润260元;
篮球 | 排球 | |
进价(元/个) | 80 | 50 |
售价(元/个) | 95 | 60 |
(1)列方程组求解:商店购进篮球和排球各多少个?
(2)销售6个排球的利润与销售几个篮球的利润相等?