��Ŀ����
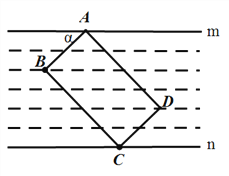
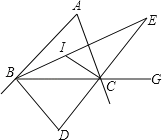
����Ŀ����ѧ��С����ѧ�������εĽ�ƽ���ߺ���������4�����⣬��������������ͼ���ڡ�ABC�У���BAC=48�㣬��I�����ǡ�ABC����ACB��ƽ���ߵĽ��㣮
��1����գ���BIC=�������� �㣮
��2������D���������ƽ���ߵĽ��㣬��գ���BDC=�������� �㣮
��3������E���ڽǡ�ABC����ǡ�ACG��ƽ���ߵĽ��㣬��̽������BEC���BAC��������ϵ����˵�����ɣ�
��4�������⣨3���������£�����ACB������������ ��ʱ��CE��AB��
���𰸡���1��114����2��66����3����BEC![]() ��BAC�����ɼ���������4��84��
��BAC�����ɼ���������4��84��
��������
��1���ȸ��������ε��ڽǺͶ��������ABC+��ACB�Ķ����������ɸ��ݽ�ƽ���ߵ�������á�IBC+��ICB�Ķ�����Ȼ�������������ε��ڽǺͶ���������������
��2������һ���ڲ��ǵ�ƽ�����ഹֱ�ɵá�IBD=��ICD=90���������ı��ε��ڽǺͿɵá�BDC+��BIC=180�����ٽ�ϣ�1����Ľ�����ô𰸣�
��3�����ACE=��ECG=x����ABI=��IBC=y�����������ε�������ʿɵ�2x=2y+��A��x=y+��E��Ȼ��������μ��ý��ۣ�
��4������ƽ���ߵ��ж��ɵõ���ECA=��A=48��ʱCE��AB��Ȼ����ݽ�ƽ���ߵ����ʺ�ƽ�ǵĶ��弴����������
�⣺��1���ߡ�A=48����
���ABC+��ACB=180����48��=132����
�ߵ�I�����ǡ�ABC����ACB��ƽ���ߵĽ��㣬
���IBC+��ICB![]() (��ABC+��ACB)=66�������BIC=180����66��=114����
(��ABC+��ACB)=66�������BIC=180����66��=114����
�ʴ�Ϊ��114��
��2����ͼ����IBƽ�֡�ABC��DBƽ�֡�FBC��
���IBD![]() (��ABC+��FBC)= 90����
(��ABC+��FBC)= 90����
ͬ���ɵá�ICD=90����
���BDC+��BIC=180����
���BDC=180������BIC=66����
�ʴ�Ϊ��66��

��3����BEC![]() ��BAC��
��BAC��
���ɣ����ACE=��ECG=x����ABI=��IBC=y��
��2x=2y+��A�٣�x=y+��E�ڣ�
�����2���ڿɵã���E![]() ��A��
��A��
��4������ECA=��A=48��ʱ��CE��AB��
��CEƽ�֡�ACG��
���ECG=��ECA=48����
���ACB=180����48����48��=84����
�ʴ�Ϊ��84��