题目内容
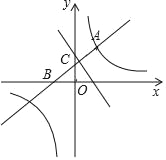
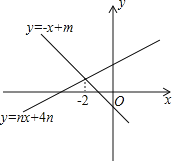
【题目】如图，直线y=-x+m与y=nx+4n（n≠0）的交点的横坐标为-2．则下列结论：①m＜0，n＞0；②直线y=nx+4n一定经过点（-4，0）；③m与n满足m=2n-2；④当x＞-2时，nx+4n＞-x+m，其中正确结论的个数是（ ）
A. 1个B. 2个C. 3个D. 4个
【答案】D
【解析】
①由直线y=-x+m与y轴交于负半轴，可得m＜0；y=nx+4n（n≠0）的图象从左往右逐渐上升，可得n＞0，即可判断结论①正确；
②将x=-4代入y=nx+4n，求出y=0，即可判断结论②正确；
③由整理即可判断结论③正确；
④观察函数图象，可知当x＞-2时，直线y=nx+4n在直线y=-x+m的上方，即nx+4n＞-x+m，即可判断结论④正确．
解：①∵直线y=-x+m与y轴交于负半轴，∴m＜0；
∵y=nx+4n（n≠0）的图象从左往右逐渐上升，∴n＞0，
故结论①正确；
②将x=-4代入y=nx+4n，得y=-4n+4n=0，
∴直线y=nx+4n一定经过点（-4，0）．
故结论②正确；
③∵直线y=-x+m与y=nx+4n（n≠0）的交点的横坐标为-2，
∴当x=-2时，y=2+m=-2n+4n，
∴m=2n-2．
故结论③正确；
④∵当x＞-2时，直线y=nx+4n在直线y=-x+m的上方，
∴当x＞-2时，nx+4n＞-x+m，
故结论④正确．
故选：D．
练习册系列答案
新思维假期作业暑假吉林大学出版社系列答案
蓝天教育暑假优化学习系列答案
相关题目
