题目内容
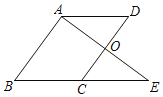
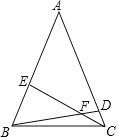
【题目】如图,在ABC中,AB=AC=10,E,D分别是AB,AC上的点,BE=4,CD=2,且BD=CE,则BD=________________.
【答案】![]()
【解析】
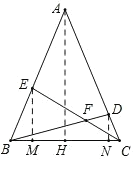
分别过点E,A,D作BC的垂线,垂足分别为M,H,C,分别证△BME∽△BHA,△EBM∽△DCN,由相似的性质推出CN![]() BM及EM与AH之间的数量关系.设BM=2a,DN=x,通过勾股定理求出a与x的值,再在Rt△BDN中,通过勾股定理即可求出BD的值.
BM及EM与AH之间的数量关系.设BM=2a,DN=x,通过勾股定理求出a与x的值,再在Rt△BDN中,通过勾股定理即可求出BD的值.
如图,分别过点E,A,D作BC的垂线,垂足分别为M,H,N,则EM∥AH∥DN,BH=CH,∴△BME∽△BHA,∴![]() ,∴设BM=2a,则BH=5a,BC=10a,∴MH=3a.
,∴设BM=2a,则BH=5a,BC=10a,∴MH=3a.
∵AB=AC,∴∠ABC=∠ACB.
又∵∠EMB=∠DNC=90°,∴△EBM∽△DCN,∴![]() 2,∴CN
2,∴CN![]() BM=a.设DN=x,则EM=2x.
BM=a.设DN=x,则EM=2x.
在Rt△EMC与Rt△DNB中,MC=8a,BN=9a,EM2+MC2=EC2,DN2+BN2=BD2.
∵BD=CE,∴EM2+MC2=DN2+BN2,即(2x)2+(8a)2=x2+(9a)2,化简得:x2![]() a2.
a2.
在Rt△DNC中,DN2+CN2=CD2,∴x2+a2=22,∴![]() a2+a2=4,化简得:a2
a2+a2=4,化简得:a2![]() ,∴x2
,∴x2![]() .
.
在Rt△BDN中,BD![]()
![]() .
.
故答案为:![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】某校有3000名学生.为了解全校学生的上学方式,该校数学兴趣小组以问卷调查的形式,随机调查了该校部分学生的主要上学方式(参与问卷调查的学生只能从以下六个种类中选择一类),并将调查结果绘制成如下不完整的统计图.
种类 | A | B | C | D | E | F |
上学方式 | 电动车 | 私家车 | 公共交通 | 自行车 | 步行 | 其他 |
某校部分学生主要上学方式扇形统计图某校部分学生主要上学方式条形统计图

根据以上信息,回答下列问题:
(1)参与本次问卷调查的学生共有____人,其中选择B类的人数有____人.
(2)在扇形统计图中,求E类对应的扇形圆心角α的度数,并补全条形统计图.
(3)若将A、C、D、E这四类上学方式视为“绿色出行”,请估计该校每天“绿色出行”的学生人数.