题目内容
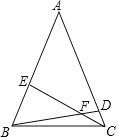
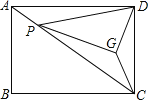
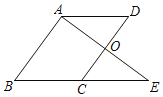
【题目】如图,在四边形ABCD中,AD∥BC,O是CD的中点,延长AO交BC的延长线于点E,且BC=CE.
(1)求证:△AOD≌△EOC;
(2)若∠BAE=90°,AB=6,OE=4,求AD的长.
【答案】(1)详见解析;(2)AD=5.
【解析】
(1)证△AOD≌△EOC,由条件推理可用AAS证明求解;
(2)求AD的长,由第(1)可知AD=EC,求CE的长需求BE,BE可由勾股定理和三角形的中位线定理求得.
解:如图所示:
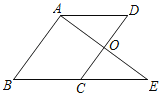
(1)∵AD∥BE,
∴∠DAE=∠AEB,
又∵O是CD的中点,
∴CO=DO,
在△AOD和△EOC中,
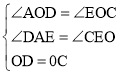 ,
,
∴△AOD≌△EOC(AAS).
(2)∵BC=CE,AO=EO
∴点C、O分别是BE和AE的中点,即CO是△ABE的中位线;
∵OE=4,∴AE=8,
又∵AB=6,
∴在Rt△ABE中,由勾股定理得:
![]() ,
,
CE=BE﹣BC=10﹣5=5.
又∵AD=EC
∴AD=5.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目