题目内容
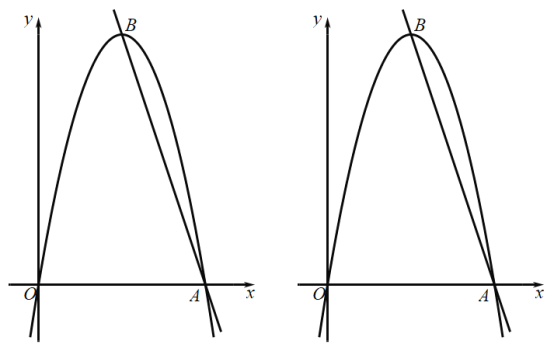
【题目】二次函数的图象过点(4,-5)和(0,3),且与x轴交于点M(-1,0)和N,
(1)求此二次函数的解析式;
(2)如果这二次函数的图像的顶点为点P,点O是坐标原点,求△OPN的面积.
(3)如果点R与点P关于x轴对称,判定以M、N、P、R为顶点的四边形的边之间的位置与度量关系.
【答案】(1)y=-x2+2x+3;(2)6;(3)该四边形(两组)对边(分别)平行,四条边都相等
【解析】
(1)将已知的三点代入,利用待定系数法即可解答;
(2)先求得点P和点N的坐标,再得出线段ON的长度以及ON边上的高,最后运用三角形面积公式解答即可;
(3)先画出图形,再说明四边形MRNP是菱形,然后运用菱形的性质解答即可.
解:(1)设二次函数的解析式为y=ax2+bx+c,
∴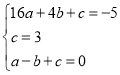 ,
,
可以解得a=-1,b=2,c=3 .
∴y=-x2+2x+3;
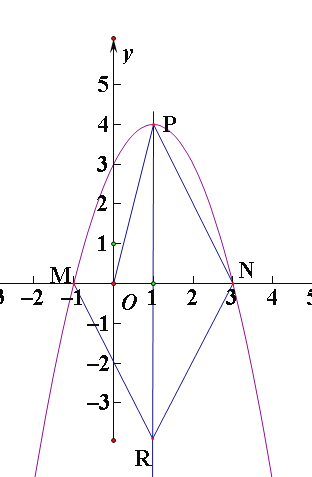
(2)如图:由题意可知二次函数的图像的顶点为点P(1,4),点N(3,0),
∴ON=3, ON边上的高为4
∴S△OPN=3×4÷2=6 .
(3)如图:∵点R与点P关于x轴对称
∴MN垂直平分PR
∵PR是二次函数的图像对称轴
∴PR垂直平分MN
∴PR互相MN垂直平分,
∴PMRN为菱形
∴该四边形(两组)对边(分别)平行,四条边都相等

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某初中学校每个年级学生刚好为500人,为了解数学史知识的普及情况,随机从每个年级各抽10名学生进行测试,测试成绩整理如下:
年级 | 学生测试成绩表 | |||||||||
七年级 | 36 | 55 | 67 | 68 | 75 | 81 | 81 | 85 | 92 | 96 |
八年级 | 45 | 66 | 72 | 77 | 80 | 84 | 86 | 92 | 95 | 96 |
九年级 | 55 | 68 | 75 | 84 | 85 | 87 | 93 | 94 | 96 | 97 |
(1)估计该校学生数学史掌握水平能达到80分以上(含80分)的人数;
(2)现从成绩在95分以上(含95分)的学生中,任取3名参加数学史学习的经验汇报,求每个年级恰好都有一名学生参加的概率.