Question

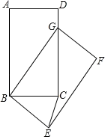
【题目】如图，AB是⊙O的直径，C，D是⊙O上两点，且，连接OC，BD，OD．

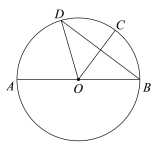
（1）求证：OC垂直平分BD；

（2）过点C作⊙O的切线交AB的延长线于点E，连接AD，CD．

①依题意补全图形；

②若AD=6，，求CD的长．

Answer 1

【答案】（1）详见解析；（2）①详见解析；②

【解析】

（1）根据等弧所对的圆心角相等可得∠COD =∠COB，由等角对等边的性质可得OD = OB，继而由线段垂直平分线的判定可求证结论；

（2）①根据题意补全图形即可；

②先根据切线的性质和题（1）可知DB∥CE，进而可得∠AEC=∠ABD，继而在Rt△ABD中，推出BD=8，AB=10，然后推导出DF=4，CF=2，继而在Rt△CFD中，由勾股定理即可求出CD的长．

（1）证明：∵

∴∠COD =∠COB．

∵OD = OB，

∴OC垂直平分BD．

（2）解：①补全图形，如图所示．

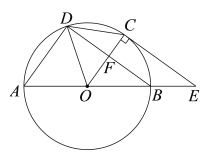
②∵CE是⊙O切线，切点为C，

∴OC⊥CE于点C．

记OC与BD交于点F，由（1）可知OC垂直BD，

∴∠OCE=∠OFB=90°．

∴DB∥CE．

∴∠AEC=∠ABD．

在Rt△ABD中，AD=6，，

∴BD=8，AB=10．

∴OA= OB=OC=5．

由（1）可知OC平分BD，即DF= BF，

∴BF=DF=4．

∴．

∴CF=2．

在Rt△CFD中，．