��Ŀ����
����Ŀ����ͼ����֪������y=�� ![]() x2+bx+c��x���ڵ�A��2��0����B��һ8��0������y���ڵ�C������A��B��C����ġ�M��y�����һ������ΪD��
x2+bx+c��x���ڵ�A��2��0����B��һ8��0������y���ڵ�C������A��B��C����ġ�M��y�����һ������ΪD��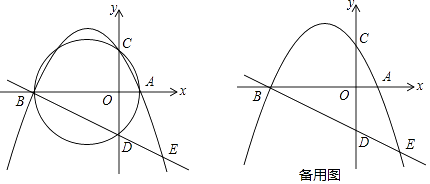
��1����������ߵı���ʽ��Բ��M�����ꣻ
��2����PΪ��BC������һ�㣨�����B��C�غϣ�������AP��y���ڵ�N�����ʣ�APAN�Ƿ�Ϊ��ֵ�����ǣ���������ֵ�������ǣ���˵�����ɣ�
��3���ӳ��߶�BD���������ڵ�E�����F���߶�BE�ϵ�����һ�㣨�����˵㣩������AF������Q�ӵ�A���������߶�AF��ÿ��1����λ���ٶ��˶�����F�������߶�FB��ÿ�� ![]() ����λ���ٶ��˶�����B��ֹͣ���ʵ���F�������Ƕ���ʱ����Q�������˶�����������ʱ�����٣�
����λ���ٶ��˶�����B��ֹͣ���ʵ���F�������Ƕ���ʱ����Q�������˶�����������ʱ�����٣�
���𰸡�
��1��
�⣺�����߽���ʽΪy=�� ![]() ��x+8����x��2����
��x+8����x��2����
��y=�� ![]() x2��
x2�� ![]() x+4��
x+4��
��x=0ʱ��y=�� ![]() x2��
x2�� ![]() x+4=4����C��0��4��
x+4=4����C��0��4��
��BC=4 ![]() ��AC=2
��AC=2 ![]() ��AB=10��
��AB=10��
��BC2+AC2=AB2��
���ABCΪֱ�������Σ��ҡ�ACB=90�㣬
��ABΪֱ����
��Բ��M�������Ϊ����3��0��
��2��
�⣺��APANΪ��ֵ���������£�
��ͼ1��
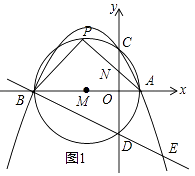
��ABΪֱ����
���APB=90�㣬
�ߡ�APB=��AON����NAO=��BAP��
���APB�ס�AON��
��AN��AB=AO��AP��
��ANAP=ABAO=20��
����APANΪ��ֵ����ֵ��20
��3��
�⣺��AB��CD��
��OD=OC=4����D��0����4����
��ֱ��BD�Ľ���ʽΪy=�� ![]() x��4��
x��4��
��F����FG��x����G����ͼ2��
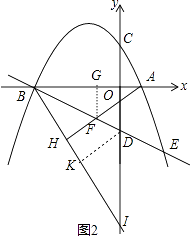
��FG��OD��
���BFG�ס�BDO��
�� ![]() =
= ![]() ����
���� ![]() =
= ![]() =
= ![]() =
= ![]() ��
��
���Q���߶�FB��ÿ�� ![]() ����λ���ٶ��˶�����B����ʱ��
����λ���ٶ��˶�����B����ʱ��
���ڵ�Q��ÿ��1����λ���ٶ��˶���G���ʱ�䣬
�൱AF+FG��ֵ��Сʱ����Q�������˶�����������ʱ�����٣�
����EBI=��ABE��BI��y����I��
��FH��BI��H����FH=FG��
��AF+FG=AF+FH��
����A��F��H����ʱ��AF+FH��ֵ��С����ʱAH��BI����ͼ2��
��DK��BI������ΪK��
��BEƽ�֡�ABI��
��DI=DO=4��
��DI=m��
�ߡ�DIK=��BIO��
���IDK�ס�IBO��
�� ![]() =
= ![]() =
= ![]() =
= ![]() ��
��
��BI=2m��
��Rt��OBI�У�82+��4+m��2=��2m��2�����m1=4����ȥ����m2= ![]() ��
��
��I��0���� ![]() ����
����
��ֱ��BI�Ľ���ʽΪy=kx+n��
��B����8��0����I��0���� ![]() �������
������� 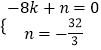 �����
����� 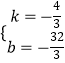 ��
��
��ֱ��BI�Ľ���ʽΪy=�� ![]() x��
x�� ![]() ��
��
��AH��BI��
��ֱ��AH�Ľ���ʽ����Ϊy= ![]() x+q��
x+q��
��A��2��0������� ![]() +q=0�����q=��
+q=0�����q=�� ![]() ��
��
��ֱ��AH�Ľ���ʽΪy= ![]() x��
x�� ![]() ��
��
�ⷽ���� 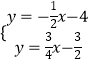 �����
����� ![]() ��
��
��F����2����3����
������F�������ǣ���2����3��ʱ����Q�������˶�����������ʱ�����٣�
����������1�����ý���ʽ��д�������߽���ʽΪy=�� ![]() x2��
x2�� ![]() x+4�������C�����꣬Ȼ�����ù��ɶ������涨��֤����ABCΪֱ�������Σ��ҡ�ACB=90�㣬�����Բ�ܽǶ��������ۿ��ж�ABΪֱ�����Ӷ��õ�Բ��M������ꣻ��2����ͼ1������Բ�ܽǶ����õ���APB=90�㣬���֤����APB�ס�AON��Ȼ���������Ʊȿɵõ�ANAP=20����APANΪ��ֵ����3���ȸ��ݴ��������õ�OD=OC=4����D��0����4������ֱ��BD�Ľ���ʽΪy=��
x+4�������C�����꣬Ȼ�����ù��ɶ������涨��֤����ABCΪֱ�������Σ��ҡ�ACB=90�㣬�����Բ�ܽǶ��������ۿ��ж�ABΪֱ�����Ӷ��õ�Բ��M������ꣻ��2����ͼ1������Բ�ܽǶ����õ���APB=90�㣬���֤����APB�ס�AON��Ȼ���������Ʊȿɵõ�ANAP=20����APANΪ��ֵ����3���ȸ��ݴ��������õ�OD=OC=4����D��0����4������ֱ��BD�Ľ���ʽΪy=�� ![]() x��4����F����FG��x����G����ͼ2��ͨ��֤����BFG�ס�BDO�õ�
x��4����F����FG��x����G����ͼ2��ͨ��֤����BFG�ס�BDO�õ� ![]() =
= ![]() =
= ![]() �����Q���߶�FB��ÿ��
�����Q���߶�FB��ÿ�� ![]() ����λ���ٶ��˶�����B����ʱ����ڵ�Q��ÿ��1����λ���ٶ��˶���G���ʱ�䣬�����жϵ�AF+FG��ֵ��Сʱ����Q�������˶�����������ʱ�����٣�����EBI=��ABE��BI��y����I����FH��BI��H����FH=FG������A��F��H����ʱ��AF+FH��ֵ��С����ʱAH��BI����ͼ2����DK��BI������ΪK����DI=m��֤����IDK�ס�IBO�õ�BI=2m��
����λ���ٶ��˶�����B����ʱ����ڵ�Q��ÿ��1����λ���ٶ��˶���G���ʱ�䣬�����жϵ�AF+FG��ֵ��Сʱ����Q�������˶�����������ʱ�����٣�����EBI=��ABE��BI��y����I����FH��BI��H����FH=FG������A��F��H����ʱ��AF+FH��ֵ��С����ʱAH��BI����ͼ2����DK��BI������ΪK����DI=m��֤����IDK�ס�IBO�õ�BI=2m��
�����ù��ɶ����õ�82+��4+m��2=��2m��2 �� ���m1=4����ȥ����m2= ![]() ���Ӷ��õ�I��0����
���Ӷ��õ�I��0���� ![]() �������������ô���ϵ����ȷ��ֱ��BI�Ľ���ʽΪy=��
�������������ô���ϵ����ȷ��ֱ��BI�Ľ���ʽΪy=�� ![]() x��
x�� ![]() ����ȷ��ֱ��AH�Ľ���ʽ��Ȼ����ֱ��BE��AH�Ľ������꼴�ɣ�
����ȷ��ֱ��AH�Ľ���ʽ��Ȼ����ֱ��BE��AH�Ľ������꼴�ɣ�