题目内容
【题目】解答题
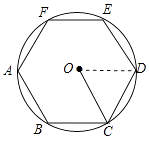
(1)如图1,在圆内接正六边形ABCDEF中,半径OC=4,求正六边形的边长. 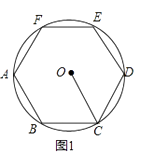
(2)如图2,在△ABC中,AB=13,BC=10,BC边上的中线AD=12.求证:AB=AC. 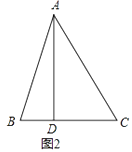
【答案】
(1)解:连接OD,如图所示:
∵六边形ABCDEF是圆O的内接正六边形,
∴∠O= ![]() =60°,
=60°,
∵OC=OD,
∴△OCD是等边三角形,
∴CD=OC=4,
即正六边形的边长为4
(2)证明:∵AD是△ABC的中线,
∴BD=CD= ![]() BC=5,
BC=5,
∵AB=13,AD=12,
∴BD2+AD2=52+122=169=132=AB2,
∴△ABD是直角三角形,AD⊥BC,
又∵BD=CD,
∴AB=AC.
【解析】(1)连接OD,求出∠O=60°,证出△OCD是等边三角形,得出CD=OC=4即可;(2)由勾股定理的逆定理证出AD⊥BC,再由线段垂直平分线的性质即可得出AB=AC.
【考点精析】解答此题的关键在于理解等腰三角形的性质的相关知识,掌握等腰三角形的两个底角相等(简称:等边对等角),以及对正多边形和圆的理解,了解圆的内接四边形的对角互补,并且任何一个外角都等于它的内对角;圆的外切四边形的两组对边的和相等.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目