Question

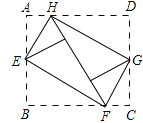
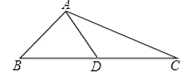
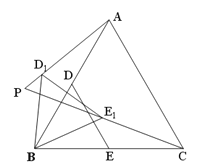
【题目】已知：在等边△ABC中， AB=， D，E分别是AB，BC的中点（如图）．若将△BDE绕点B逆时针旋转，得到△BD1E1，设旋转角为α（0°＜α＜180°），记射线CE1与AD1的交点为P．点P到BC所在直线的距离的最大值为_____________．

Answer 1

【答案】2

【解析】∵等边△ABC，∴∠ABC=60°，AB=CB，

∵等边△D1E1B，∴∠D1BE1=60°，D1B= BE1，

∴∠D1BA=∠E1BC，

在△D1BA和△E1BC中，

，

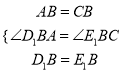∴△D1BA≌△E1BC（SAS），

∴∠PAB=∠PCB，

∵∠APC+∠PAB=∠ABC+∠PCB，

∴∠APC=∠ABC=60°，

∵∠D1BE1=60°，

∴P、B、E1、D1共圆，

当BP⊥BC时，点P 到BC所在直线距离最大，此时E1恰好在AB上且为AB中点，

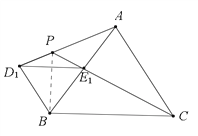
∵E1为AB中点，

∴E1C平分∠ACB，

∴∠PCB=30°，

∵tan30°==,

∴PB=BC×=2×=2.

故答案为2.