题目内容
【题目】在平面直角坐标系中，点A（0，a）、B（b，0）．
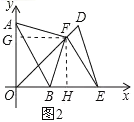
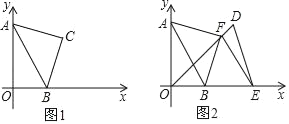
（1）若a、b满足a2+b2﹣8a﹣4b+20=0．如图，在第一象限内以AB为斜边作等腰Rt△ABC，请求四边形AOBC的面积S；
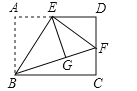
（2）如图，若将线段AB沿x轴向正方向移动a个单位得到线段DE（D对应A，E对应B）连接DO，作EF⊥DO于F，连接AF、BF，判断AF与BF的关系，并说明理由．
【答案】(1)9;(2) 结论：FA=FB，FA⊥FB，理由见解析.
【解析】
（1）根据非负数的性质列出算式，求出a、b的值；根据等腰直角三角形的性质求出AC、BC，根据三角形的面积公式计算即可；
（2）作FG⊥y轴，FH⊥x轴垂足分别为G、H，证明四边形FHOG是正方形，得到OG=FH，∠GFH=90°，证明△AFG≌△BFH，根据全等三角形的性质计算即可．
解：（1）∵a2+b2-8a-4b+20=0，
∴（a-4）2+（b-2）2=0，
∴a=4，b=2；即A（0，4），B（2，0），
∴AB=
=2
∵△ABC是等腰直角三角形，
∴AC=BC=
,
∴四边形AOBC的面积S=
×OA×OB+×AC×BC=4+5=9；
（2）
结论：FA=FB，FA⊥FB，理由如下：
如图2，作FG⊥y轴，FH⊥x轴垂足分别为G、H，
∵A（0，a）向右平移a个单位到D，
∴点D坐标为（a，a），点E坐标为（a+b，0），
∴∠DOE=45°，
∵EF⊥OD，
∴∠OFE=90°，∠FOE=∠FEO=45°，
∴FO=EF，
∴FH=OH=HE=（a+b），
∴点F坐标为（
，），
∴FG=FH，四边形FHOG是正方形，
∴OG=FH=，∠GFH=90°，
∴AG=AO-OG=a-=
，BH=OH-OB=-b=，
∴AG=BH，
在△AFG和△BFH中，
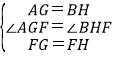
∴△AFG≌△BFH，
∴FA=FB，∠AFG=∠BFH，
∴∠AFB=∠AFG+∠BFG=∠BFH+∠BFG=90°，
∴FA=FB，FA⊥FB．
