题目内容
【题目】如图1,在平面直角坐标系中,![]() ,将线段
,将线段![]() 平移得到线段
平移得到线段![]() ,点
,点![]() 的坐标为
的坐标为![]() ,连结
,连结![]() .
.
(1)点![]() 的坐标为__________________(用含
的坐标为__________________(用含![]() 的式子表示);
的式子表示);
(2)若![]() 的面积为4,求点
的面积为4,求点![]() 的坐标;
的坐标;
(3)如图2,在(2)的条件下,延长![]() 交
交![]() 轴于点
轴于点![]() ,延长
,延长![]() 交
交![]() 轴于
轴于![]() ,
,![]() 是
是![]() 轴上一动点,
轴上一动点,![]() 的值记为
的值记为![]() ,在点
,在点![]() 运动的过程中,
运动的过程中,![]() 的值是否发生变化,若不变,请求出
的值是否发生变化,若不变,请求出![]() 的值,并写出此时
的值,并写出此时![]() 的取值范围,若变化,说明理由.
的取值范围,若变化,说明理由.
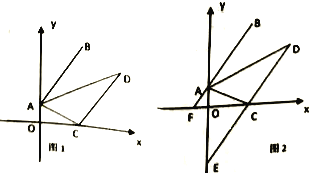
【答案】(1)![]() ;(2)D(4,3);(3)当
;(2)D(4,3);(3)当![]() 时,
时,![]() ,变化;当
,变化;当![]() 时,
时,![]() ,不变;当
,不变;当![]() 时,
时,![]() ,变化.
,变化.
【解析】
(1)各对应点之间的关系是横坐标加m,纵坐标减1,即可得到结论;(2)(2)如图1中,作DH⊥OC于H.根据S△ADC=S梯形ADHO-S△AOC-S△DCH,计算即可.
(3)分三种情形:①如图2-1中,当t<-![]() 时.②如图2-2中,当-
时.②如图2-2中,当-![]() ≤t≤2时.③如图2-3中,当t>2时,分别求解即可.
≤t≤2时.③如图2-3中,当t>2时,分别求解即可.
解:
(1)由![]() 平移到
平移到![]() ,可得平移后各对应点之间的关系是横坐标加m,纵坐标减1,所以
,可得平移后各对应点之间的关系是横坐标加m,纵坐标减1,所以![]() 平移后坐标为
平移后坐标为![]() ;
;
(2)如图1中,作DH⊥OC于H.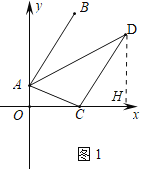
∵S△ADC=S梯形ADHO-S△AOC-S△DCH,
∴![]() (1+3)(m+2)-
(1+3)(m+2)-![]() ×1×m-
×1×m-![]() ×2×3=4,
×2×3=4,
解得m=2,
∴D(4,3).
(3)①如图2-1中,当t<-![]() 时,S=2-3t,变化.
时,S=2-3t,变化.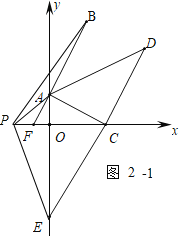
理由:由题意P(t,0),E(0,-3),C(2,0),F(-![]() ,0),B(2,4).A(0,1).
,0),B(2,4).A(0,1).
S=S△PAB+S△PEC=S△PBF-S△PAF+S△PCE=![]() (-
(-![]() -t)(4-1)+
-t)(4-1)+![]() (2-t)3=2-3t.
(2-t)3=2-3t.
②如图2-2中,当-![]() ≤t≤2时,s=4不变.
≤t≤2时,s=4不变.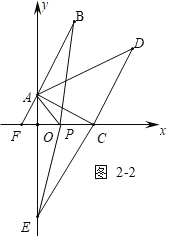
理由:S=S△PAB+S△PEC=S△PBF-S△PAF+S△PCE=![]() (t+
(t+![]() )(4-1)+
)(4-1)+![]() (2-t)3=4.
(2-t)3=4.
③如图2-3中,当t>2时,S=3t-2变化.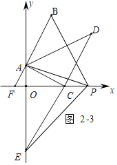
理由:S=S△PAB+S△PEC=S△PBF-S△PAF+S△PCE=![]() (t+
(t+![]() )(4-1)+
)(4-1)+![]() (t-2)3=3t-2.
(t-2)3=3t-2.