题目内容
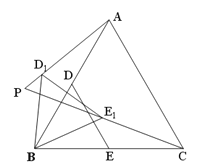
【题目】如图,抛物线m:y=﹣0.25(x+h)2+k与x轴的交点为A,B,与y轴的交点为C,顶点为M(3,6.25),将抛物线m绕点B旋转180°,得到新的抛物线n,它的顶点为D.
(1)求抛物线n的解析式;
(2)设抛物线n与x轴的另一个交点为E,点P是线段DE上一个动点(P不与D,E重合),过点P作y轴的垂线,垂足为F,连接EF.如果P点的坐标为(x,y),△PEF的面积为S,求S与x的函数关系式,写出自变量x的取值范围,并求出S的最大值;
(3)设抛物线m的对称轴与x轴的交点为G,以G为圆心,A,B两点间的距离为直径作⊙G,试判断直线CM与⊙G的位置关系,并说明理由.

【答案】(1)y=![]() x2﹣
x2﹣![]() x+36;(2)S=﹣
x+36;(2)S=﹣![]() x2+
x2+![]() x(13<x<18),△PEF的面积S没有最大值;(3)直线CM与⊙G相切,理由见解析.
x(13<x<18),△PEF的面积S没有最大值;(3)直线CM与⊙G相切,理由见解析.
【解析】试题分析:(1)根据抛物线m的顶点为M(3,6.25)得出m的解析式为y=-![]() (x-3)2+
(x-3)2+![]() =-
=-![]() (x-8)(x+2),求出A(-2,0),B(8,0),再根据旋转的性质得出D的坐标为(13,-6.25),进而求出抛物线n的解析式;
(x-8)(x+2),求出A(-2,0),B(8,0),再根据旋转的性质得出D的坐标为(13,-6.25),进而求出抛物线n的解析式;
(2)由点E与点A关于点B成中心对称,得出E(18,0),利用待定系数法求出直线DE的解析式为y=![]() x-
x-![]() ,再根据S△PEF=
,再根据S△PEF=![]() PFOF得出S与x的函数关系式,进而求解即可;
PFOF得出S与x的函数关系式,进而求解即可;
(3)利用勾股定理求出CG=![]() =5=⊙G的半径,得出点C在⊙G上.过M作y轴的垂线,垂足为N,连结CM,利用勾股定理求出CM2=CN2+MN2=(
=5=⊙G的半径,得出点C在⊙G上.过M作y轴的垂线,垂足为N,连结CM,利用勾股定理求出CM2=CN2+MN2=(![]() -4)2+32=
-4)2+32=![]() ,计算得出CG2+CM2=52+
,计算得出CG2+CM2=52+![]() =
=![]() =(
=(![]() )2=GM2,根据勾股定理的逆定理得到CG⊥CM,由切线的判定定理即可得出直线CM与⊙G相切.
)2=GM2,根据勾股定理的逆定理得到CG⊥CM,由切线的判定定理即可得出直线CM与⊙G相切.
试题解析:(1)∵抛物线m:y=﹣0.25(x+h)2+k的顶点为M(3,6.25),
∴m的解析式为y=﹣![]() (x﹣3)2+
(x﹣3)2+![]() =﹣
=﹣![]() (x﹣8)(x+2),
(x﹣8)(x+2),
∴A(﹣2,0),B(8,0),
∵将抛物线m绕点B旋转180°,得到新的抛物线n,它的顶点为D,
∴D的坐标为(13,﹣6.25),
∴抛物线n的解析式为y=![]() (x﹣13)2﹣
(x﹣13)2﹣![]() ,即y=
,即y=![]() x2﹣
x2﹣![]() x+36;
x+36;
(2)∵点E与点A关于点B成中心对称,
∴E(18,0).
设直线DE的解析式为y=kx+b,
则 ,解得
,解得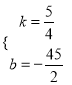
∴y=![]() x﹣
x﹣![]() ,
,
∵P点的坐标为(x,y),13<x<18,
∴S△PEF=![]() PFOF=
PFOF=![]() x(﹣y)=﹣
x(﹣y)=﹣![]() xy=﹣
xy=﹣![]() x(
x(![]() x﹣
x﹣![]() )=﹣
)=﹣![]() x2+
x2+![]() x,
x,
即S=﹣![]() x2+
x2+![]() x(13<x<18),
x(13<x<18),
∴当x= =9时,S有最大值,但13<x<18,所以△PEF的面积S没有最大值;
=9时,S有最大值,但13<x<18,所以△PEF的面积S没有最大值;
(3)直线CM与⊙G相切,理由如下:
∵抛物线m的解析式为y=﹣![]() (x﹣3)2+
(x﹣3)2+![]() =﹣
=﹣![]() (x﹣8)(x+2),
(x﹣8)(x+2),
∴令x=0,得y=4,
∴C(0,4).
∵抛物线m的对称轴与x轴的交点为G,
∴G(3,0),
∵OC=4,OG=3,连结CG,
∴CG=![]() =5,
=5,
∵AB=10,
∴⊙G的半径是5,
∴点C在⊙G上.
过M作y轴的垂线,垂足为N,连结CM,
则CM2=CN2+MN2=(![]() ﹣4)2+32=
﹣4)2+32=![]() ,
,
又CG2+CM2=52+![]() =
=![]() =(
=(![]() )2=GM2,
)2=GM2,
∴CG⊥CM,
∴直线CM与⊙G相切.


 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案