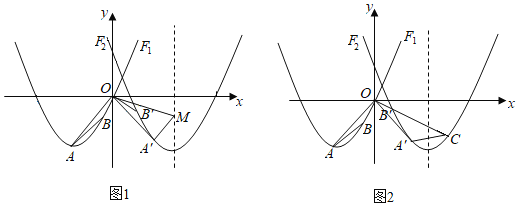题目内容
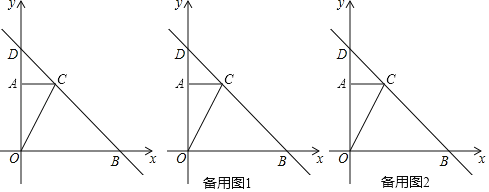
【题目】如图,在平面直角坐标系中,Rt△AOC的直角边OA在y轴正半轴上,且顶点O与坐标原点重合,点C的坐标为(1,2),直线y=﹣x+b过点C,与x轴交于点B,与y轴交于点D.
(1)B点的坐标为 ,D点的坐标为 ;
(2)动点P从点O出发,以每秒1个单位长度的速度,沿O→A→C的路线向点C运动,同时动点Q从点B出发,以相同速度沿BO的方向向点O运动,过点Q作QH⊥x轴,交线段BC或线段CO于点H.当点P到达点C时,点P和点Q都停止运动,在运动过程中,设动点P运动的时间为t秒:
①设△CPH的面积为S,求S关于t的函数关系式;
②是否存在以Q、P、H为顶点的三角形的面积与S相等?若存在,直接写出t的值;若不存在,请说明理由.
【答案】(1)(3,0);(0,3);(2)①S=  ;②存在,t=1或
;②存在,t=1或![]() 时,以Q、P、H为顶点的三角形的面积与S相等.
时,以Q、P、H为顶点的三角形的面积与S相等.
【解析】
(1)把点C坐标代入直线求得b的值即得到直线解析式,令y=0求点B坐标,令x=0求点D坐标.
(2)①由Rt△AOC中∠OAC=90°求得OA+AC=OB=3,即t的取值范围为0≤t<3且t≠2.画图发现有两种情况:当0≤t<2时,点P在线段OA上,点H在线段BC上,可证得PH∥x轴,故S=S△CPH=![]() PHAP,用t表示PH、AP的值再代入即能用t表示S;当2<t<3时,点P在线段AC上,点H在线段OC上,此时以PC为底、点H到CP距离h为高来求S,用t表示CP、h的值再代入即能用t表示S.再把两式统一写成S关于t的分段函数关系式.
PHAP,用t表示PH、AP的值再代入即能用t表示S;当2<t<3时,点P在线段AC上,点H在线段OC上,此时以PC为底、点H到CP距离h为高来求S,用t表示CP、h的值再代入即能用t表示S.再把两式统一写成S关于t的分段函数关系式.
②与①类似把点P、Q的位置分两种情况讨论计算;其中P在AC上、H在OC上时,以QH为底求△QPH的面积,需对点P到QH的距离PE的表示再进行一次分类.用t表示△QPH面积后与S相等列得方程,解之求得t的值.
解:(1)∵直线y=﹣x+b过点C(1,2)
∴﹣1+b=2
∴b=3,即直线为y=﹣x+3
当y=0时,﹣x+3=0,得x=3;当x=0时,y=3
∴B(3,0),D(0,3)
故答案为:(3,0);(0,3).
(2)①∵Rt△AOC中,∠OAC=90°,C(1,2)
∴A(0,2),OA=2,AC=1
∵OB=OD=3,∠BOD=90°
∴OA+AC=OB=3,∠OBD=45°
∴0≤t<3,且t≠2
i)当0≤t<2时,点P在线段OA上,点H在线段BC上,如图1
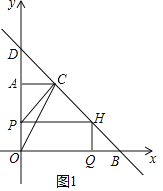
∴OP=BQ=t
∴AP=OA﹣OP=2﹣t,OQ=OB﹣BQ=3﹣t
∵HQ⊥x轴于点Q
∴∠BQH=90°
∴△BQH是等腰直角三角形
∴HQ=BQ=t
∴HQ∥OP且HQ=OP
∴四边形OPHQ是平行四边形
∴PH∥x轴,PH=OQ=3﹣t
∴S=S△CPH=![]() PHAP=
PHAP=![]() (3﹣
(3﹣![]() t2﹣
t2﹣![]() t+3
t+3
ii)当2<t<3时,点P在线段AC上,点H在线段OC上,如图2

∴CP=OA+AC﹣t=3﹣t,xH=OQ=3﹣t
∵直线OC解析式为:y=2x
∴QH=yH=2(3﹣t)=6﹣2t
∴点H到CP的距离h=2﹣(6﹣2t)=2t﹣4
∴S=S△CPH=![]() CPh=
CPh=![]() (3﹣t)(2t﹣4)=﹣t2+5t﹣6
(3﹣t)(2t﹣4)=﹣t2+5t﹣6
综上所述,S关于t的函数关系式为S= 
②存在以Q、P、H为顶点的三角形的面积与S相等.
i)当0≤t<2时,如图3
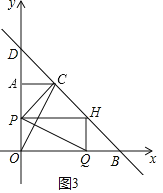
∵S△CPH=S△QPH,两三角形有公共底边为PH
∴点C和点Q到PH距离相等,即AP=OP
∴t=2﹣t
∴t=1
ii)当2<t≤2.5时,如图4,延长QH交AC于点E
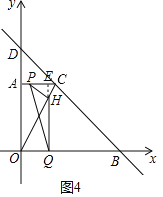
∴AE=OQ=3﹣t,AP=t﹣2,QH=6﹣2t
∴PE=AE﹣AP=(3﹣t)﹣(t﹣2)=5﹣2t
∴S△QPH=![]() QHPE=
QHPE=![]() (6﹣2t)(5﹣2t)=2t2﹣11t+15
(6﹣2t)(5﹣2t)=2t2﹣11t+15
∵S△CPH=S△QPH
∴﹣t2+5t﹣6=2t2﹣11t+15
解得:t1=3(舍去),t2=![]()
iii)当2.5<t<3时,如图5,延长QH交AC于点E

∴PE=AP﹣AE=(t﹣2)﹣(3﹣t)=2t﹣5
∴S△QPH=![]() QHPE=
QHPE=![]() (6﹣2t)(2t﹣5)=﹣2t2+11t﹣15
(6﹣2t)(2t﹣5)=﹣2t2+11t﹣15
∴﹣t2+5t﹣6=﹣2t2+11t﹣15
解得:t1=t2=3(舍去)
综上所述,t=1或![]() 时,以Q、P、H为顶点的三角形的面积与S相等.
时,以Q、P、H为顶点的三角形的面积与S相等.

【题目】为拓展学生视野,促进书本知识与生活实践的深度融合,荆州市某中学组织八年级全体学生前往松滋洈水研学基地开展研学活动.在此次活动中,若每位老师带队14名学生,则还剩10名学生没老师带;若每位老师带队15名学生,就有一位老师少带6名学生,现有甲、乙两种大型客车,它们的载客量和租金如表所示:
甲型客车 | 乙型客车 | |
载客量(人/辆) | 35 | 30 |
租金(元/辆) | 400 | 320 |
学校计划此次研学活动的租金总费用不超过3000元,为安全起见,每辆客车上至少要有2名老师.
(1)参加此次研学活动的老师和学生各有多少人?
(2)既要保证所有师生都有车坐,又要保证每辆车上至少要有2名老师,可知租车总辆数为 辆;
(3)学校共有几种租车方案?最少租车费用是多少?