题目内容
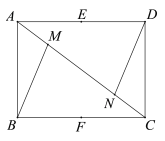
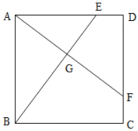
【题目】如图,正方形ABCD,点E,F分别在AD,CD上,且DE=CF,AF与BE相交于点G.
(1)求证:BE=AF;
(2)若AB=4,DE=1,求AG的长.
【答案】(1)见解析;(2)![]()
【解析】
(1)由正方形的性质得出∠BAE=∠ADF=90°,AB=AD=CD,得出AE=DF,由SAS证明△BAE≌△ADF,即可得出结论;
(2)由全等三角形的性质得出∠EBA=∠FAD,得出∠GAE+∠AEG=90°,因此∠AGE=90°,由勾股定理得出BE=![]() ,在Rt△ABE中,由三角形面积即可得出结果.
,在Rt△ABE中,由三角形面积即可得出结果.
(1)证明:∵四边形ABCD是正方形,
∴∠BAE=∠ADF=90°,AB=AD=CD,
∵DE=CF,
∴AE=DF,
在△BAE和△ADF中,
∵ ,
,
![]() ,
,
![]() ,
,
(2)由(1)得:△BAE≌△ADF,
∴∠EBA=∠FAD,
∴∠GAE+∠AEG=90°,
∴∠AGE=90°,
∵AB=4,DE=1,
∴AE=3,
![]() ,
,
在![]() 中,
中,![]()
![]() ,
,

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】“倡导全民阅读”“推动国民素质和社会文明程度显著提高”已成为“十三五”时期的重要工作.某中学在全校学生中随机抽取了部分学生对2018年度阅读情况进行问卷调查,并将收集的数据统计如表
数量/本 | 15 | 11 | 8 | 4 | 3 | 2 |
人数 | 80 | 60 | 50 | 100 | 40 | 70 |
根据表中的信息判断,下列结论错误的是( )
A. 该校参与调查的学生人数为400人
B. 该校学生2018年度阅读书数量的中位数为4本
C. 该校学生2018年度阅读书数量的众数为4本
D. 该校学生2018年平均每人阅读8本书