Question

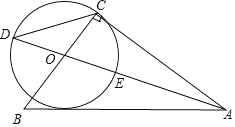
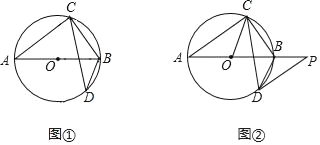
【题目】如图1，已知⊙O外一点P向⊙O作切线PA，点A为切点，连接PO并延长交⊙O于点B，连接AO并延长交⊙O于点C，过点C作，分别交PB于点E，交⊙O于点D，连接AD．

（1）求证：△APO～△DCA；

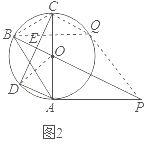
（2）如图2，当时

①求的度数；

②连接AB，在⊙O上是否存在点Q使得四边形APQB是菱形．若存在，请直接写出的值；若不存在，请说明理由．

Answer 1

【答案】（1）见解析；（2）①；②存在，.

【解析】

（1）由切线性质和直径AC可得，由可得，即可得：；

（2）①连接OD，由可得△OAD是等边三角形，由此可得，；

②作交⊙O于Q，可证ABQP为菱形，求可转化为求．

（1）∵PA切⊙O于点A，AC是⊙O的直径，

∴，

∵，

∴，

∴，

∴，

∴，

∴，

（2）如图2，连接OD，

①∵ ，，

∴△是等边三角形，

∴，

∵，

∴，

∵，

∴，

②存在．如图2，过点B作交⊙O于Q，连接PQ，BC，CQ，

由①得：，，

∴，

∵，

∴，

∴，

∵，

∴，

∵，

∴

∴

∵

∴，

∴，

∵，

∴，

∴四边形ABQP是平行四边形，

∵，

∴四边形ABQP是菱形，

∴

∴，