Question

【题目】如图1，对角线互相垂直的四边形叫做垂美四边形．

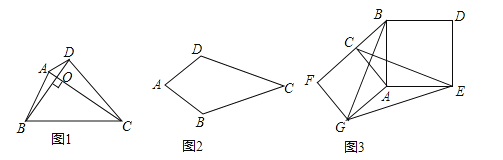
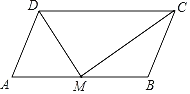
(1)概念理解：如图2，在四边形中，，，问四边形是垂美四边形吗？请说明理由；

(2)性质探究：如图1，四边形的对角线、交于点，．试证明：；

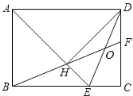
(3)解决问题：如图3，分别以的直角边和斜边为边向外作正方形和正方形，连结、、．已知，，求的长．

Answer 1

【答案】(1) 四边形是垂美四边形，理由见解析；(2)证明见解析；(3) .

【解析】

（1）根据垂直平分线的判定定理，可证直线是线段的垂直平分线，结合“垂美四边形”的定义证明即可；

（2）根据垂直的定义和勾股定理解答即可；

（3）连接、，先证明，得到∴，可证，即，从而四边形是垂美四边形，根据垂美四边形的性质、勾股定理、结合（2）的结论计算即可．

(1)四边形是垂美四边形．

证明：连接AC，BD，

∵，

∴点在线段的垂直平分线上，

∵，

∴点在线段的垂直平分线上，

∴直线是线段的垂直平分线，

∴，即四边形是垂美四边形；

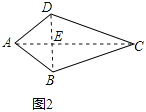
(2)猜想结论：垂美四边形的两组对边的平方和相等．

如图2，已知四边形中，，垂足为，

求证：

证明：∵，

∴，

由勾股定理得，，

，

∴；

故答案为：．

(3)连接、，

∵，

∴，即，

在和中，，

∴，

∴，又，

∴，即，

∴四边形是垂美四边形，

由(2)得，，

∵，，

∴，，，

∴，

∴．