题目内容
【题目】如图:在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF;证明: 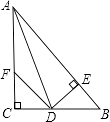
(1)CF=EB.
(2)AB=AF+2EB.
【答案】
(1)证明:∵AD是∠BAC的平分线,DE⊥AB,DC⊥AC,
∴DE=DC,
在Rt△CDF和Rt△EDB中,
![]() ,
,
∴Rt△CDF≌Rt△EDB(HL).
∴CF=EB
(2)证明:∵AD是∠BAC的平分线,DE⊥AB,DC⊥AC,
∴CD=DE.
在△ADC与△ADE中,
![]() ,
,
∴△ADC≌△ADE(HL),
∴AC=AE,
∴AB=AE+BE=AC+EB=AF+CF+EB=AF+2EB.
【解析】(1)根据角平分线的性质“角的平分线上的点到角的两边的距离相等”,可得点D到AB的距离=点D到AC的距离即CD=DE.再根据Rt△CDF≌Rt△EDB,得CF=EB;(2)利用角平分线性质证明∴△ADC≌△ADE,AC=AE,再将线段AB进行转化.

练习册系列答案
相关题目