题目内容
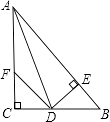
【题目】如图1,抛物线y=ax2﹣10ax+c经过△ABC的三个顶点,已知BC∥x轴,点A在x轴上,点C在y轴上,OA= ![]() 且AC=BC.
且AC=BC.
(1)求抛物线的解析式;
(2)如图2,将△AOC沿x轴对折得到△AOC1,再将△AOC1绕平面内某点旋转180°后得△A1O1C2(A,O,C1分别与点A1,O1,C2对应)使点A1,C2在抛物线上,求A1,C2的坐标.
(3)如图3,若Q为直线AB上一点,直接写出|QC﹣QD|的取值范围.
【答案】(1)![]() ;(2)A1(16,0),C2(10,8);(3)0≤ |QC﹣QD|≤12
;(2)A1(16,0),C2(10,8);(3)0≤ |QC﹣QD|≤12
【解析】(1)令x=0,求出C的坐标,根据对称求出B的坐标,由已知条件求出得A(-6,0),B(10,8),C(0,8)代入解析式即可求出解析式;(2)由抛物线的对称性得到:对称轴与x轴的交点M为对称中心,求出A1、C2的坐标;(3)根据若Q为直线AB上一点,即可写出|QC﹣QD|的取值范围.
解:(1)由抛物线对称轴为x=5且BC∥x轴
得BC=10,由OA=![]() 且AC=BC.
且AC=BC.
得A(-6,0),B(10,8),C(0,8)
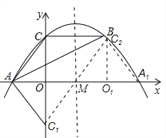
得y=![]()
(2) 由抛物线的对称性得到:对称轴与x轴的交点M为对称中心,
根据对称性得到:C1M=C2M,AM=A1M,
得A1(16,0),C2(10,8)
(3)0≤ |QC﹣QD|≤12(注:少一个等于号扣1分)
“点睛”此题属于二次函数的综合题,涉及的知识有:二次函数的性质,利用待定系数法函数的解析式,点的坐标,等腰三角形的性质,线段垂直平分线的性质,线段的中点坐标公式,勾股定理,以及折叠、旋转的性质,利用了转化,分类讨论数形结合的思想,是一道综合性强、较难的题,要求学生作掌握知识要全面.

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目