题目内容
在△ABC中,∠B=35°,AD是BC边上的高,并且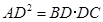 ,则∠BCA的度数为 。
,则∠BCA的度数为 。
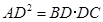 ,则∠BCA的度数为 。
,则∠BCA的度数为 。55°或125°
试题分析:分两种情况考虑:当∠BCA为锐角和钝角,将已知的积的恒等式化为比例式,再根据夹角为直角相等,利用两边对应成比例且夹角的相等的两三角形相似可得出△ADB∽△CDA,由相似三角形的对应角相等,利用直角三角形的两锐角互余及外角性质分别求出两种情况下∠BCA的度数即可.

当∠BCA为锐角时,如图1所示,
∵
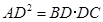 ,
,∴
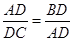 ,
,又AD⊥BC,
∴∠ADB=∠CDA=90°,
∴△ADB∽△CDA,又∠B=35°,
∴∠CAD=∠B=35°,∠BCA=∠BAD,
在Rt△ADB中,∠ADB=90°,∠B=35°,
∴∠BAD=55°,
则∠BCA=∠BAD=55°;
当∠BCA为钝角时,如图2所示,
同理可得△ADB∽△CDA,又∠B=35°,
可得∠CAD=∠B=35°,
则∠BCA=∠CDA+∠CAD=125°,
综上,∠BCA的度数为55°或125°.
点评:相似三角形的判定和性质是初中数学的重点,贯穿于整个初中数学的学习,是中考中比较常见的知识点,一般难度不大,需熟练掌握.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


 ,结果精确到0.1海里)
,结果精确到0.1海里) ,BC=3,△DEF是边长为a(a为小于3的常数)的等边三角形,将△DEF沿AC方向平移,使点D在线段AC上,DE∥AB,设△DEF与△ABC重叠部分的周长为T。
,BC=3,△DEF是边长为a(a为小于3的常数)的等边三角形,将△DEF沿AC方向平移,使点D在线段AC上,DE∥AB,设△DEF与△ABC重叠部分的周长为T。
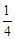 ,当a=2时,求T的值;
,当a=2时,求T的值;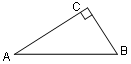

 的根,则判别式△=b2-4ac和完全平方式M=
的根,则判别式△=b2-4ac和完全平方式M= 的关系是( )
的关系是( )