题目内容
某校要把一块形状是直角三角形的废地开发为生物园。如图所示,∠ACB=90°,AC=80m,BC=60m。若线段CD为一条水渠,且D在边AB上,已知水渠的造价是10元/米,则D点在距A点多远处时此水渠的造价最低?最低造价是多少?在图上标出D点。

480元,如下图
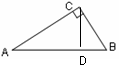

试题分析:过C作CD⊥AB于D,先根据勾股定理求得AB的长,然后由直角三角形的面积公式根据等面积法即可求得CD的长,最后在Rt△ACD中根据勾股定理即可求得结果.
解:过C作CD⊥AB于D

∵∠ACB=90°,AC=80m,BC=60m
∴AB=
 =100m
=100m由面积相等得
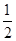 AB·CD=
AB·CD=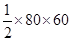 ,解得CD=48
,解得CD=48在Rt△ACD中,AD=
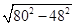 =64
=64距A点64m时造价最低,最低价是
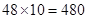 元.
元.点评:勾股定理的应用是初中数学的重点,贯穿于整个初中数学的学习,是中考中比较常见的知识点,一般难度不大,需熟练掌握.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
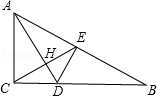
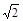
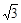
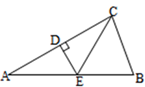
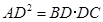 ,则∠BCA的度数为 。
,则∠BCA的度数为 。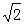 ,P是AC上的一个动点.
,P是AC上的一个动点.