Question

【题目】（1）在等边三角形ABC中，

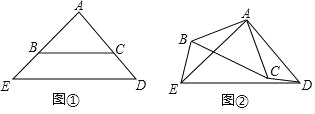
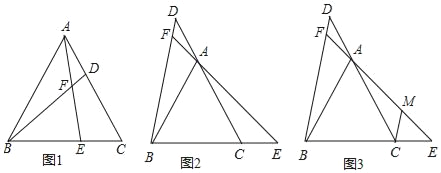
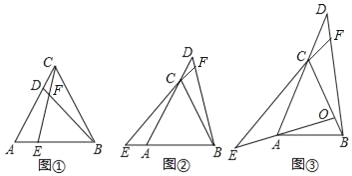
①如图①，D，E分别是边AC，AB上的点且AE=CD，BD与EC交于点F，则∠BFE的度数是　 　度；

②如图②，D，E分别是边AC，BA延长线上的点且AE=CD，BD与EC的延长线交于点F，此时∠BFE的度数是　 　度；

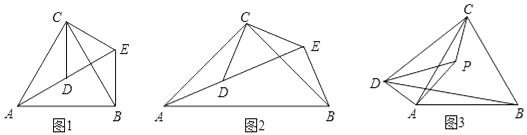
（2）如图③，在△ABC中，AC=BC，∠ACB是锐角，点O是AC边的垂直平分线与BC的交点，点D，E分别在AC，OA的延长线上，AE=CD，BD与EC的延长线交于点F，若∠ACB=α，求∠BFE的大小．（用含α的代数式表示）．

Answer 1

【答案】（1）①60°；②60°；（2）∠BFE =α．

【解析】

（1）①先证明△ACE≌△CBD得到∠ACE=∠CBD，再由三角形外角和定理可得∠BFE=∠CBD+∠BCF；②先证明△ACE≌△CBD得∠ACE=∠CBD=∠DCF，再由三角形外角和定理可得∠BFE=∠D+∠DCF=∠D+∠CBD=∠BCA；

（2）证明△AEC≌△CDB得到∠E=∠D，则∠BFE=∠D+∠DCF=∠E+∠ECA=∠OAC=α．

（1）如图①中，

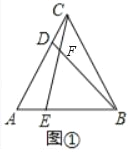
∵△ABC是等边三角形，

∴AC=CB，∠A=∠BCD=60°，

∵AE=CD，

∴△ACE≌△CBD，

∴∠ACE=∠CBD，

∴∠BFE=∠CBD+∠BCF=∠ACE+∠BCF=∠BCA=60°．

故答案为60．

（2）如图②中，

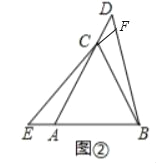
∵△ABC是等边三角形，

∴AC=CB，∠A=∠BCD=60°，

∴∠CAE=∠BCD=′120°

∵AE=CD，

∴△ACE≌△CBD，

∴∠ACE=∠CBD=∠DCF，

∴∠BFE=∠D+∠DCF=∠D+∠CBD=∠BCA=60°．

故答案为60．

（3）如图③中，

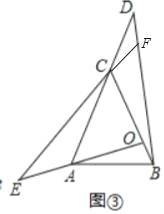
∵点O是AC边的垂直平分线与BC的交点，

∴OC=OA，

∴∠EAC=∠DCB=α，

∵AC=BC，AE=CD，

∴△AEC≌△CDB，

∴∠E=∠D，

∴∠BFE=∠D+∠DCF=∠E+∠ECA=∠OAC=α．