题目内容
【题目】(1)问题发现
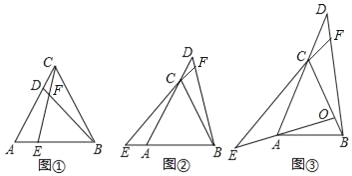
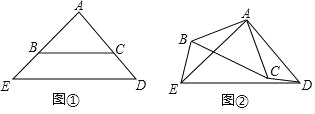
如图①,△ABC和△AED都是等腰直角三角形,∠BAC=∠EAD=90°,点B在线段AE上,点C在线段AD上,请直接写出线段BE与线段CD的数量关系: ;
(2)操作探究
如图②,将图①中的△ABC绕点A顺时针旋转,旋转角为α(0<α<360),请判断线段BE与线段CD的数量关系,并说明理由.
【答案】(1)BE=CD;(2)BE=CD;证明见解析.
【解析】
(1)根据等腰直角三角形的性质可得AB=AC,AE=AD,再根据等量关系可得线段BE与线段CD的关系;
(2)根据等腰直角三角形的性质可得AB=AC,AE=AD,根据旋转的性质可得∠BAE=∠CAD,根据SAS可证△BAE≌△CAD,根据全等三角形的性质即可求解;
解:(1)BE=CD,理由如下;
∵△ABC和△AED都是等腰直角三角形,∠BAC=∠EAD=90°,
∴AB=AC,AE=AD,
∴AE﹣AB=AD﹣AC,
∴BE=CD;
故答案为:BE=CD.
(2)∵△ABC和△AED都是等腰直角三角形,∠BAC=∠EAD=90°,
∴AB=AC,AE=AD,
由旋转的性质得,∠BAE=∠CAD,
在△BAE与△CAD中,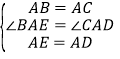 ,
,
∴△BAE≌△CAD(SAS)
∴BE=CD.

练习册系列答案
相关题目
【题目】一辆出租车从A地出发,在一条东西走向的街道上往返,每次行驶的情况(记向东为正)记录如下(x>5且x<14,单位:m):
行驶次数 | 第一次 | 第二次 | 第三次 | 第四次 |
行驶情况 | x | ﹣ | x﹣3 | 2(5﹣x) |
行驶方向(填“东”或“西”) |
|
|
|
|
(1)请将表格补充完整;
(2)求经过连续4次行驶后,这辆出租车所在的位置;
(3)若出租车行驶的总路程为41m,求第一次行驶的路程x的值.