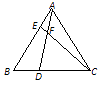题目内容
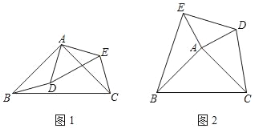
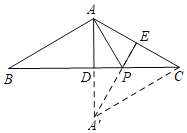
【题目】如图，在等腰△ABC中，AB=AC，BC=8，∠BAC=120°，作AD⊥BC于点D，AD=
AB，点E为边AC上的中点，点P为BC上一动点，则PA+PE的最小值为_______．
【答案】4
【解析】
先作出点A的对称点A'：延长AD至A'，使AD=A'D，连接A'E，交BC于P，此时PA+PE的值最小，就是A'E的长，证明CD=A'E=4即可．
解：∵AB=AC，BC=8，AD⊥BC，
∴BD=CD=4，
∵
∴∠B=
30°，
∴∠BAD=∠CAD=60°，
延长AD至A'，使AD=A'D，连接A'E，交BC于P，
此时PA+PE的值最小，就是A'E的长，
∵AD=
AB，AA′=2AD，
∴AA'=AB=AC，∠CAA'=60°，
∴△AA'C是等边三角形，
∵E是AC的中点，
∴A'E⊥AC，
∴A'E=CD=4，
即PA+PE的最小值是4，
故答案为：4．
【题目】某年级共有300名学生，为了解该年级学生在
，
两个体育项目上的达标情况，进行了抽样调査．过程如下，请补充完整．
收集数据从该年级随机抽取30名学生进行测试，测试成绩（百分制）如下：
项目 78 86 74 81 75 76 87 49 74 91 75 79 81 71 74 81 86 69 83 77 82 85 92 95 58 54 63 67 82 74
项目 93 73 88 81 72 81 94 83 77 83 80 81 70 81 73 78 82 100 70 40 84 86 92 96 53 57 63 68 81 75
整理、描述数据
项目的频数分布表
分组 | 划记 | 频数 |
| — | 1 |
|
| 2 |
|
| 2 |
|
| 8 |
| ||
|
| 5 |
（说明：成绩80分及以上为优秀，60～79分为基本达标，59分以下为不合格）
根据以上信息，回答下列问题：
（1）补全统计图、统计表；
（2）在此次测试中，成绩更好的项目是__________，理由是__________；
（3）假设该年级学生都参加此次测试，估计项目和项目成绩都是优秀的人数最多为________人．
