题目内容
【题目】已知,等腰△ABC和等腰△ADE中,∠BAC=∠DAE=90°.
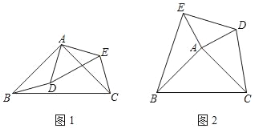
(1)如图1,求证:DB=CE;
(2)如图2.求证:S△ACD=S△ABE.
【答案】(1)见解析;(2)见解析.
【解析】
(1)根据SAS证明△BAD≌△CAE即可解决问题;
(2)如图2中,取CD的中点M,连接AM,延长AM到N,使得MN=AM,连接DN,CN.首先证明四边形ACND是平行四边形,再证明△BAE≌△ACN即可.
(1)证明:如图1中,
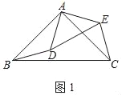
∵等腰△ABC和等腰△ADE中,∠BAC=∠DAE=90°,
∴AB=AC,AD=AD,∠BAD=∠CAE,
∴△BAD≌△CAE(SAS),
∴BD=CE.
(2)证明:如图2中,取CD的中点M,连接AM,延长AM到N,使得MN=AM,连接DN,CN.
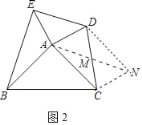
∵AM=MN,DM=CM,
∴四边形ACND是平行四边形,
∴AD=CN,AD∥CN,
∴∠DAC+∠ACN=180°,
∵∠BAC=∠EAD=90°,
∴∠BAE+∠DAC=180°,
∴∠BAE=∠ACN,
∵AB=AC,AE=AD=CN,
∴△BAE≌△ACN(SAS),
∴S△BAE=S△ACN,
∵DN∥AC,
∴S△ADC=S△ACN,
∴S△BAE=S△ADC.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目