题目内容
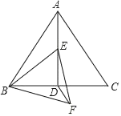
【题目】已知,如图,在等边△ABC中,点D、E分别在边BC、AB上,且 BD=AE,AD与CE交于点 ![]() .
.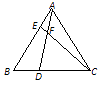
(1)试说明 ![]() 的理由;
的理由;
(2)求 ![]() 的度数.
的度数.
【答案】
(1)证明:∵△ABC是等边三角形,
∴∠BAC=∠B=60°,AB=AC.
又∵AE=BD,
∴△AEC≌△BDA(SAS).
∴AD=CE.
(2)解:由(1)知△AEC≌△BDA,
∴∠ACE=∠BAD,
∴∠DFC=∠FAC+∠ACF=∠FAC+∠BAD=∠BAC=60°.
【解析】(1)由等边三角形懂得性质得出∠BAC=∠B=60°,AB=AC,再由AE=BD,根据SAS得到△AEC≌△BDA.由全等三角形的性质得出AD=CE.
(2)由(1)知△AEC≌△BDA,根据全等三角形的性质得出∠ACE=∠BAD,再根据三角形外角性质得到∠DFC=∠FAC+∠ACF=∠FAC+∠BAD=∠BAC=60°.
【考点精析】本题主要考查了等边三角形的性质的相关知识点,需要掌握等边三角形的三个角都相等并且每个角都是60°才能正确解答此题.

练习册系列答案
相关题目