题目内容
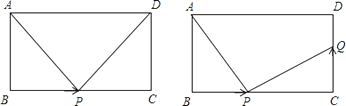
【题目】如图，笔直的公路上A、B两点相距25km，C、D为两村庄，DA⊥AB于点A，CB⊥AB于点B，已知DA=15km，CB=10km，现在要在公路的AB段上建一个土特产品收购站E，使得C、D两村到收购站E的距离相等，则收购站E应建在离A点多远处？
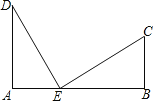
【答案】10km
【解析】
根据使得C，D两村到E站的距离相等，需要DE=CE，再根据勾股定理表示出DE2、CE2，然后列方程求解即可.
解：∵使得C，D两村到E站的距离相等．
∴DE=CE，
∵DA⊥AB于A，CB⊥AB于B，
∴∠A=∠B=90°，
∴AE2+AD2=DE2，BE2+BC2=EC2，
∴AE2+AD2=BE2+BC2，
设AE=x，则BE=AB-AE=（25-x），
∵DA=15km，CB=10km，
∴x2+152=（25-x）2+102，
解得：x=10，
∴AE=10km，
∴收购站E应建在离A点10km处．
练习册系列答案
名师点睛字词句段篇系列答案
相关题目
