题目内容
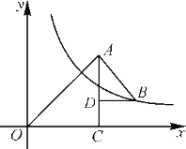
【题目】如图,在正方形ABCD中,点E是边BC的中点,连接AE、DE,分别交BD、AC于点P、Q,过点P作PF⊥AE交CB的延长线于F,下列结论:
①∠AED+∠EAC+∠EDB=90°,
②AP=FP,
③AE=![]() AO,
AO,
④若四边形OPEQ的面积为4,则该正方形ABCD的面积为36,
⑤CEEF=EQDE.
其中正确的结论有( )

A.5个B.4个C.3个D.2个
【答案】B
【解析】
①正确:证明∠EOB=∠EOC=45°,再利用三角形的外角的性质即可得出答案;
②正确:利用四点共圆证明∠AFP=∠ABP=45°即可;
③正确:设BE=EC=a,求出AE,OA即可解决问题;
④错误:通过计算正方形ABCD的面积为48;
⑤正确:利用相似三角形的性质证明即可.
①正确:如图,连接OE,
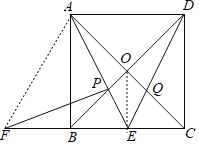
∵四边形ABCD是正方形,
∴AC⊥BD,OA=OC=OB=OD,
∴∠BOC=90°,
∵BE=EC,
∴∠EOB=∠EOC=45°,
∵∠EOB=∠EDB+∠OED,∠EOC=∠EAC+∠AEO,
∴∠AED+∠EAC+∠EDO=∠EAC+∠AEO+∠OED+∠EDB=90°,故①正确;
②正确:如图,连接AF,

∵PF⊥AE,
∴∠APF=∠ABF=90°,
∴A,P,B,F四点共圆,
∴∠AFP=∠ABP=45°,
∴∠PAF=∠PFA=45°,
∴PA=PF,故②正确;
③正确:设BE=EC=a,则AE=![]() a,OA=OC=OB=OD=
a,OA=OC=OB=OD=![]() a,
a,
∴![]() ,即AE=
,即AE=![]() AO,故③正确;
AO,故③正确;
④错误:根据对称性可知,![]() ,
,
∴![]() =
=![]()
![]() =2,
=2,
∵OB=OD,BE=EC,
∴CD=2OE,OE⊥CD,
∴![]()
![]() ,
, ![]() ,
,
∴![]() ,
, ![]() ,
,
∴![]() ,
,
∴![]() ,故④错误;
,故④错误;
⑤正确:∵∠EPF=∠DCE=90°,∠PEF=∠DEC,
∴![]() ,
,
∴![]() ,
,
∴EQ=PE,
∴CEEF=EQDE,故⑤正确;
综上所诉一共有4个正确,故选:B.

 阅读快车系列答案
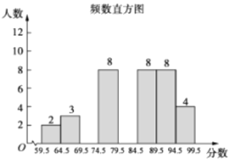
阅读快车系列答案【题目】随着“微信运动”被越来越多的人关注和喜爱,某数学兴趣小组随机调查了我区50名教师某日“微信运动”中的步数情况进行统计整理,绘制了如下的统计图表(不完整):
步数 | 频数 | 频率 |
0≤x<4000 | 8 | 0.16 |
4000≤x<8000 | 15 | 0.3 |
8000≤x<12000 | 12 | a |
12000≤x<16000 | b | 0.2 |
16000≤x<20000 | 3 | 0.06 |
20000≤x<24000 | 2 | 0.04 |
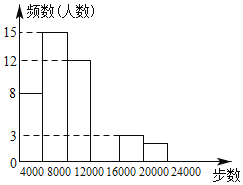
请根据以上信息,解答下列问题:
(1)写出a,b的值并补全频数分布直方图;
(2)我市约有5000名教师,用调查的样本数据估计日行走步数超过12000步(包含12000步)的教师有多少名?
(3)若在50名被调查的教师中,选取日行走步数超过16000步(包含16000步)的两名教师与大家分享心得,用树形图或列表法求被选取的两名教师恰好都在20000步(包含20000步)以上的概率.