题目内容
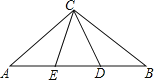
【题目】如图,△ABC中,AC=AD,BC=BE,∠ACB=100°,则∠ECD=( )
A.20°B.30°C.40°D.50°
【答案】C
【解析】
首先设∠ACE=x°,∠DCE=y°,∠BCD=z°,由BE=BC,AD=AC,利用等腰三角形的性质,即可用x,y,z表示出∠ADC与∠BEC的度数,又由三角形外角的性质,得到∠A与∠B的值,然后由在△ABC中,∠ACB=100°,利用三角形内角和定理得到方程,继而求得∠DCE的大小.
设∠ACE=x°,∠DCE=y°,∠BCD=z°,
∵BE=BC,AD=AC,
∴∠ADC=∠ACD=∠ACE+∠DCE=(x+y)°,∠BEC=∠BCE=∠BCD+∠DCE=(y+z)°,
∴∠A=∠BEC﹣∠ACE=(y+z﹣x)°,∠B=∠ADC﹣∠BCD=(x+y﹣z)°,
∵在△ABC中,∠ACB=100°,
∴∠A+∠B=180°﹣∠ACB=80°,
∴y+z﹣x+x+y﹣z=80,
即2y=80,
∴y=40,
∴∠DCE=40°.
故选C.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目





