题目内容
P(x，y)是以坐标原点为圆心，5为半径的圆周上的点，若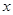
，
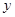都是整数，则这样的点共有（）
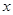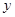，都是整数，则这样的点共有（）| A．4个 | B．8个 | C．12个 | D．16个 |
C
试题分析：应分为两种情况：①若这个点在坐标轴上，那么有四个；②若这个点在象限内，由
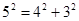，可知在每个象限有两个，总共12个．分为两种情况；
①若这个点在坐标轴上，那么有四个，它们是（0，5），（5，0），（-5，0），（0，-5）；
②若这个点在象限内，
∵
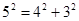，而P都是整数点，∴这样的点有8个，分别是（3，4），（3，-4），（-3，4），（-3，-4）），（4，3），（4，-3），（-4，3），（-4，-3）．
∴共12个，故选C．
点评：解答本题的关键是由题意得出分为两种不同的情况，再由勾股定理解决问题．
练习册系列答案
相关题目
