Question

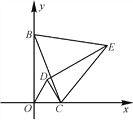
【题目】如图（1），在平面直角坐标系中，直线交y轴于点A，交x轴于点B，点C坐标为，作点C关于直线AB的对称点F，连接BF和OF，OF交AC于点E，交AB于点M．

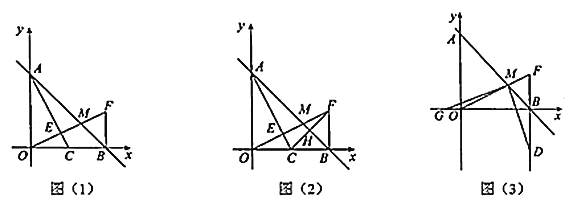
（1）求证：．

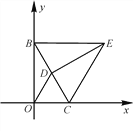
（2）如图（2），连接CF交AB于点H，求证：．

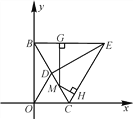
（3）如图（3），若，G为x轴负半轴上一动点，连接MG，过点M作GM的垂线交FB的延长线于点D，GB-BD的值是否为定值？若是，求其值；若不是，求其取值范围．

Answer 1

【答案】（1）见解析；（2）见解析；（3）是，

【解析】

（1）先求出A，B的坐标，再通过对称得到FB=BC且垂直x轴，从而证Rt△OAC≌Rt△FOB，得到OF⊥AC．
（2）利用勾股定理和等腰直角三角形的性质分别求出BA，BF，BH即可．
（3）过M点作MN⊥x轴于N点，MH⊥DF于H点，证明直角△MEN≌直角△MDH．

（1）证明由得，

.

关于AB对称，

，

.

又.

.

，

，即.

（2）证明：在中，，

，

在中，，

.

（3）解：GB-BD的值是定值，定值等于.

直线AB的解析式为，

点F的坐标为，直线OF的解析式为.

解方程组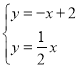得，

.

过点M作轴于点N，于点H，如图

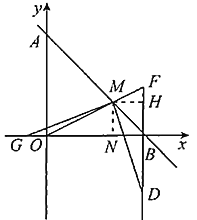
四边形MNBH是正方形，

.

又

，

，

.

在和中，，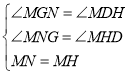

.

.

综上所述，GB-BD的值为定值.