Question

【题目】(14分)如图1，已知点B(0，6)，点C为x轴上一动点，连接BC，△ODC和△EBC都是等边三角形．

　　

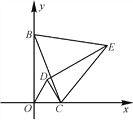
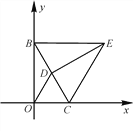
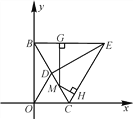
　　图1　　　　　　　　　　图2　　　　　　　 　　　图3

(1)求证：DE＝BO；

(2)如图2，当点D恰好落在BC上时．

①求OC的长及点E的坐标；

②在x轴上是否存在点P，使△PEC为等腰三角形？若存在，写出点P的坐标；若不存在，说明理由；

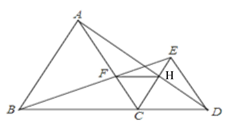
③如图3，点M是线段BC上的动点(点B，C除外)，过点M作MG⊥BE于点G，MH⊥CE于点H，当点M运动时，MH＋MG的值是否发生变化？若不会变化，直接写出MH＋MG的值；若会变化，简要说明理由．

Answer 1

【答案】(1)见解析 (2)① , ②存在 , ③不会变化，MH＋MG＝6

【解析】试题分析：（1）根据等边三角形的性质得到BC=CE，OC=CD，∠OCD=∠BCE=60°，求得∠OCB=∠DCE，根据全等三角形的性质即可得到结论；

（2）①由点B（0，6），得到OB=6，根据全等三角形的性质得到∠CDE=∠BOC=90°，根据等边三角形的性质得到∠DEC=30°，求得CE=4，过E作EF⊥x轴于F，角三角形即可得到结论；②存在，如图d，当CE=CP=4时，当CE=PE，根据等腰三角形的性质即可得到结论；③不会变化，如图c，连接EM，根据三角形的面积公式即可得到结论．

试题解析：(1)证明：∵△ODC和△EBC都是等边三角形，

∴OC＝DC，BC＝CE，∠OCD＝∠BCE＝60°.

∴∠BCE＋∠BCD＝∠OCD＋∠BCD，

即∠ECD＝∠BCO.

∴△DEC≌△OBC(SAS)．

∴DE＝BO.

(2)①∵△ODC是等边三角形，

∴∠OCB＝60°.

∵∠BOC＝90°，

∴∠OBC＝30°.

设OC＝x，则BC＝2x，

∴x2＋62＝(2x)2.解得x＝2.

∴OC＝2，BC＝4.

∵△EBC是等边三角形，

∴BE＝BC＝4.

又∵∠OBE＝∠OBC＋∠CBE＝90°，

∴E(4，6)．

②若点P在C点左侧，则CP＝4，OP＝4－2＝2，点P的坐标为(－2，0)；

若点P在C点右侧，则OP＝2＋4＝6，点P的坐标为(6，0)．

③不会变化，MH＋MG＝6.