题目内容
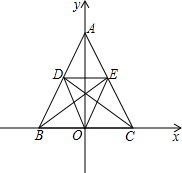
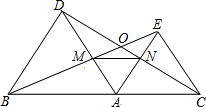
如图,在直角坐标系中,点B坐标为(-4,0),点C与点B关于原点O对称,点A为y轴上一动点,其坐标为(0,k),BE,CD分别为△ABC中AC,AB边上的高,垂足分别为E,D.
(1)当k=-3时,求AB的长;
(2)试说明△DOE是等腰三角形;
(3)k取何值时,△DOE是等边三角形?(直接写出k的值即可)
(1)当k=-3时,求AB的长;
(2)试说明△DOE是等腰三角形;
(3)k取何值时,△DOE是等边三角形?(直接写出k的值即可)

(1)∵点B坐标为(-4,0),当k=-3时,A的坐标为(0,-3),
∴OA=3,OB=4,
∴AB=
=5;
(2)∵点C与点B关于原点O对称,
∴OB=OC,
∵BE是△ABC中AC边上的高,
∴OE=
,
同理OD=
,
∴OD=OE,
∴△DOE是等腰三角形;
(3)当△ABC是锐角三角形,点A在y轴的正半轴时,
若△ODE为等边三角形,则∠DOE=60°,
∵∠BOD=∠COE=60°,
∵OD=OB,
∴∠DBO=60°,
∴∠BAO=30°,
∴AB=2BO=8,
∴OA=
=
=4
,
∴k=4
,
当点A在y轴的负半轴时,
k=-4
,
如图: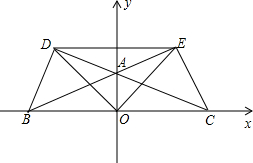 当△ABC是钝角三角形时,
当△ABC是钝角三角形时,
若△ODE为等边三角形,则∠DOE=60°,
∵∠BOD=∠COE,
∴∠COE=60°,
∵OE=OB,
∴∠OBE=∠OEB=30°,
∴AB=2AO=2|k|,
k2+42=(2k)2,
k=±
;
则k=±
或±4
.
∴OA=3,OB=4,
∴AB=
| 32+42 |
(2)∵点C与点B关于原点O对称,
∴OB=OC,
∵BE是△ABC中AC边上的高,
∴OE=
| BC |
| 2 |
同理OD=
| BC |
| 2 |
∴OD=OE,
∴△DOE是等腰三角形;
(3)当△ABC是锐角三角形,点A在y轴的正半轴时,
若△ODE为等边三角形,则∠DOE=60°,
∵∠BOD=∠COE=60°,
∵OD=OB,
∴∠DBO=60°,
∴∠BAO=30°,
∴AB=2BO=8,
∴OA=
| AB2-BO2 |
| 82-42 |
| 3 |
∴k=4
| 3 |
当点A在y轴的负半轴时,
k=-4
| 3 |
如图:
 当△ABC是钝角三角形时,
当△ABC是钝角三角形时,若△ODE为等边三角形,则∠DOE=60°,
∵∠BOD=∠COE,
∴∠COE=60°,
∵OE=OB,
∴∠OBE=∠OEB=30°,
∴AB=2AO=2|k|,
k2+42=(2k)2,
k=±
| 4 |
| 3 |
| 3 |
则k=±
| 4 |
| 3 |
| 3 |
| 3 |

练习册系列答案
相关题目
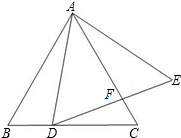
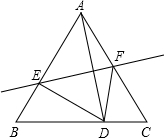 作AD的垂直平分线分别与边AB、AC交于点E、F.
作AD的垂直平分线分别与边AB、AC交于点E、F.